Biofysische grenzen: exponentiële groei
WILLIAM OPHULS
Vertaling door Gertjan Cobelens van hoofdstuk 2 van Immoderate Greatness: Why Civilizations Fail, 2012.
.
Waarom vertonen beschavingen telkens weer de neiging om de natuurlijke wereld op te vatten als een hoorn des overvloeds? Als een banket waaraan men zich naar believen tegoed kan doen? Deze dwaling komt grotendeels doordat mensen niet goed in staat zijn om de aard en de kracht van exponentiële groei te onderkennen.*
Wanneer een bank bijvoorbeeld samengestelde rente uitkeert, wordt de rente toegevoegd aan de hoofdsom, die vervolgens weer de basis vormt voor de volgende renteberekening. Een inleg van 100 euro op een spaarrekening die jaarlijks 7,2 procent samengestelde rente uitkeert, zal aan het eind van het eerste jaar 107,20 euro waard zijn, aan het eind van het tweede jaar 114,92, net zolang totdat er aan het eind van jaar tien 200,42 euro op staat. (Een handige vuistregel is dat de verdubbelingstijd in jaren grofweg gelijkstaat aan 72 gedeeld door het groeipercentage. Bij 7,2 procent is de verdubbelingstijd dus 72 gedeeld door 7,2, oftewel 10 jaar.) En er is slechts nog eens 70 jaar van samengestelde rente nodig voordat het oorspronkelijke bedrag is uitgegroeid van 100 euro tot 25.600 euro. In 80 jaar, grofweg de duur van een mensenleven, neemt de inleg met maar liefst 25.500 procent toe. Dát is de kracht van de exponentiële functie, zoals in de grafiek hieronder indringend tot uiting komt.
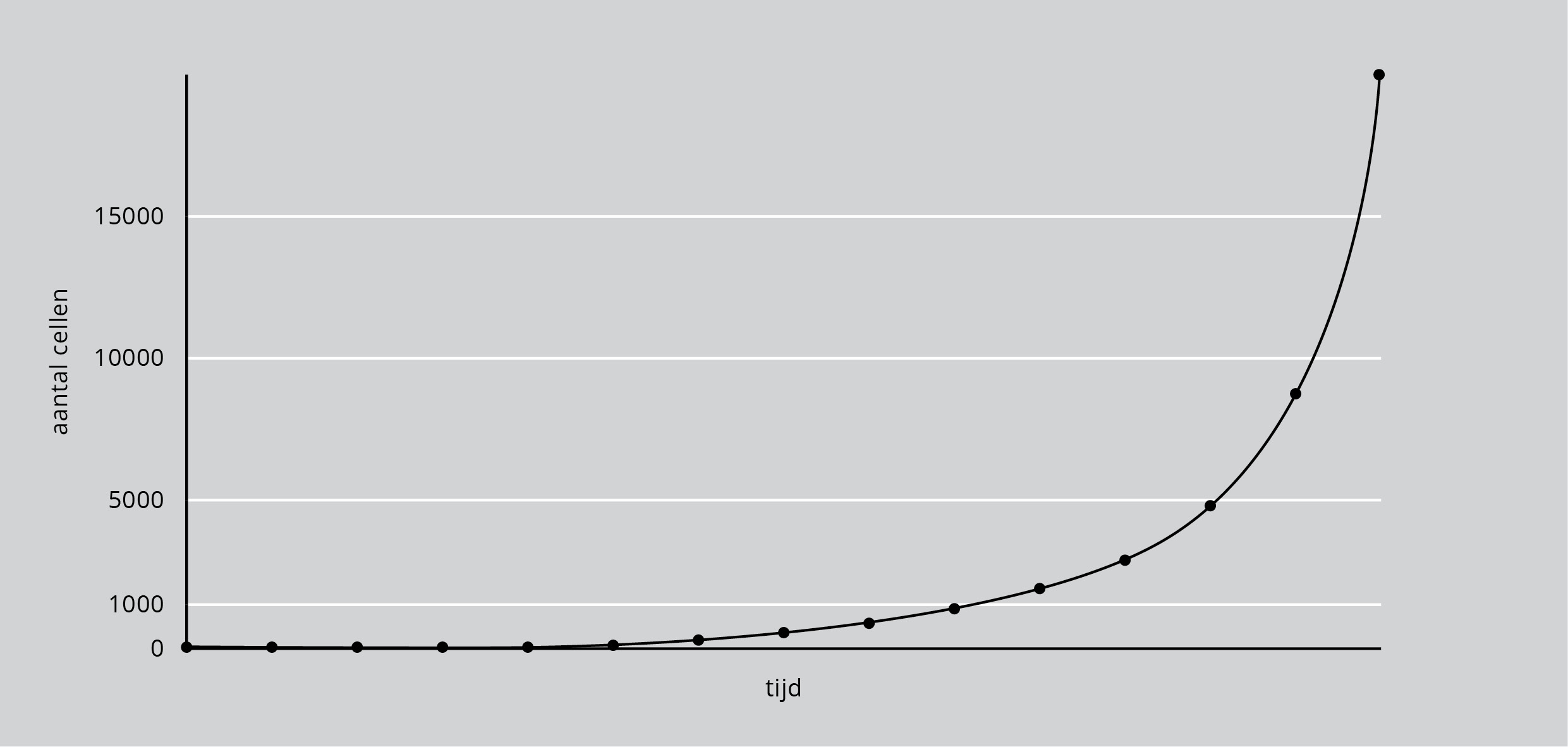
Figuur 1: Een spaarrekening met een samengestelde rente, vermenigvuldiging van bacteriën of cellen, het maakt niet uit, het resultaat is een exponentiële curve.
Om hetzelfde fenomeen vanuit een andere invalshoek te belichten, stel je een bacterie voor die zich elke tien minuten in tweeën splitst. Na tien minuten delen die twee bacteriën zich in vieren, om in slechts tien verdubbelingen de volgende progressie door te maken: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024. Nog eens tien verdubbelingen verandert die duizend in een miljoen, en nog eens tien stappen katapulteert het miljoen naar een miljard. In slechts vijf uur tijd heeft die eerste bacterie zich een miljard keer verdubbeld.
Een oude Indiase parabel verschaft ons nog een voorbeeld van de buitengewone kracht van samengestelde groei. Een hoveling die de koning een waardevolle dienst had bewezen, vroeg om een ogenschijnlijk onbeduidende beloning: één graankorrel op het eerste veld van een schaakbord, twee op het tweede, vier op het derde, acht op het vierde, helemaal tot aan het 64ste veld. De vizier van de koning rook echter onraad en berekende snel dat, als elk vakje op het bord conform de wens van de hoveling met graankorrels gevuld zou worden, daar grofweg 18 triljoen (dat wil zeggen, 18 gevolgd door 18 nullen) graankorrels voor nodig zouden zijn – een astronomisch aantal, veel meer dan de totale mondiale hoeveelheid graan. De uitgekookte hoveling betaalde er met zijn leven voor.
De grafiek is niets anders dan de eerste helft van de S-curve.

.
De parabel van de graankorrels laat zien hoeveel moeite we er mee hebben om in onze reactie de exponentiële functie een stap voor te blijven: het aantal graankorrels op het vierde veld is een korrel meer dan alle korrels op de voorgaande drie velden (1+2+4=7+1=8). En deze verhouding is een constante: het aantal korrels op het achtste veld (128) is er een meer dan het geheel van het aantal korrels op de voorgaande zeven velden (127). Met andere woorden, de hoeveelheid die in een reeks van verdubbelingen voor elke volgende verdubbeling nodig is, is altijd een fractie meer dan de som van alle voorafgaande groei.*
Neem een stad met honderdduizend inwoners die vanaf de dag dat ze gesticht is vijf bossen heeft moeten kappen om in de behoefte aan brandstof te voorzien. Als deze stad door wil groeien, zal ze onderweg naar de tweehonderdduizendste inwoner nog eens vijf bossen moeten omhakken. Anders gezegd, wanneer we aannemen dat de stad in hetzelfde tempo blijft groeien, dan zal een verdubbeling van honderdduizend naar tweehonderdduizend inwoners net zoveel hout vergen als ze tijdens haar hele geschiedenis verbruikt heeft – maar wel in slechts een zesde van de tijd.
Samengevat gaat exponentiële groei, zoals de voorgaande grafiek illustreert, gepaard met steeds grotere vermeerderingen die zich ook nog eens in een steeds hoger tempo voltrekken.
In omgekeerde richting boet deze wetmatigheid niets aan kracht in. Bij een inflatie van 3,6 procent bedraagt de koopkracht van een euro over honderd jaar slechts drie eurocent – een waardeverlies van 97 procent in een eeuw tijd. En de uitputting van grondstoffen volgt eenzelfde stramien: een mijn die een miljoen ton erts bevat en waaruit jaarlijks een vaste hoeveelheid van 10 duizend ton wordt gedolven, zal een eeuw meegaan. Neemt de gewonnen hoeveelheid echter exponentieel toe, dan is de mijn in een paar decennia uitgeput.
De les die uit deze voorbeelden kan worden getrokken is dat exponentiële groei een even sluipend als explosief proces is.
Exponentiële groei overvalt je onverhoeds en komt dan met een knal tot ontploffing.

.
Een simpel gedachte-experiment illustreert beide aspecten en verduidelijkt het eraan verbonden gevaar.
Stel je voor, het is elf uur ’s avonds en we stoppen een enkele bacterie van een soort die zich eens per minuut opdeelt in een fles van een formaat dat na precies een uur vol is. Wanneer is de fles dan halfvol? Om precies één minuut voor middernacht.
Haal nu je toverstaf tevoorschijn en maak de fles vier keer zo groot. Hoeveel tijd win je dan? Vrijwel geen: een minuut na middernacht zullen de bacteriën de helft van de fles vullen, en nog een minuut later is de fles alweer vol.
Met een veel grotere fles beginnen is geen echte oplossing omdat de groei inmiddels overweldigende vormen heeft aangenomen. Een fles die 32 keer zo groot is als de oorspronkelijke zal om vijf minuten na middernacht gevuld zijn. En zelfs een fles van duizend keer het oorspronkelijke formaat zit om tien over twaalf tjokvol! Met andere woorden, een toverstaf stelt het onvermijdelijke slechts uit: exponentiële groei is een tsunami die alles op zijn pad verzwelgt.
Stel nu dat het absoluut noodzakelijk is om te voorkomen dat de fles vol raakt. Wanneer moeten we dan in de verdubbelingssnelheid van de bacteriën ingrijpen? Om vijf voor twaalf vullen de bacteriën nog maar drie procent van de fles, dus wat zouden we ons druk maken? Zelfs een fles die voor een kwart gevuld is, vormt geen directe aanleiding tot ongerustheid, aangezien er nog ruim voldoende tijd voorhanden lijkt om op te treden – ook al is het in werkelijkheid al twee voor twaalf. Is de fles echter halfvol, dan wordt de situatie serieus nijpend: we hebben nu nog maar één minuut om in te grijpen.
Ik wil er nogmaals op wijzen dat groei zich zowel sluipenderwijs als explosief voltrekt. Net als bij een tsunami blijft de energie die zich ophoopt onopgemerkt, totdat het water uit zee oprijst en de mensen op de oever overspoelt. Hoe snel de impact van groei overweldigende vormen aanneemt, is niet alleen een functie van het groeitempo in relatie tot de grenzen van het systeem, maar ook van de managementvaardigheden en de technologische competentie van een samenleving. Maar aangezien ‘groter groeien’ in de genen van elke beschaving besloten ligt, is de vraag niet òf, maar wanneer groei de vorm van een tsunami aanneemt.
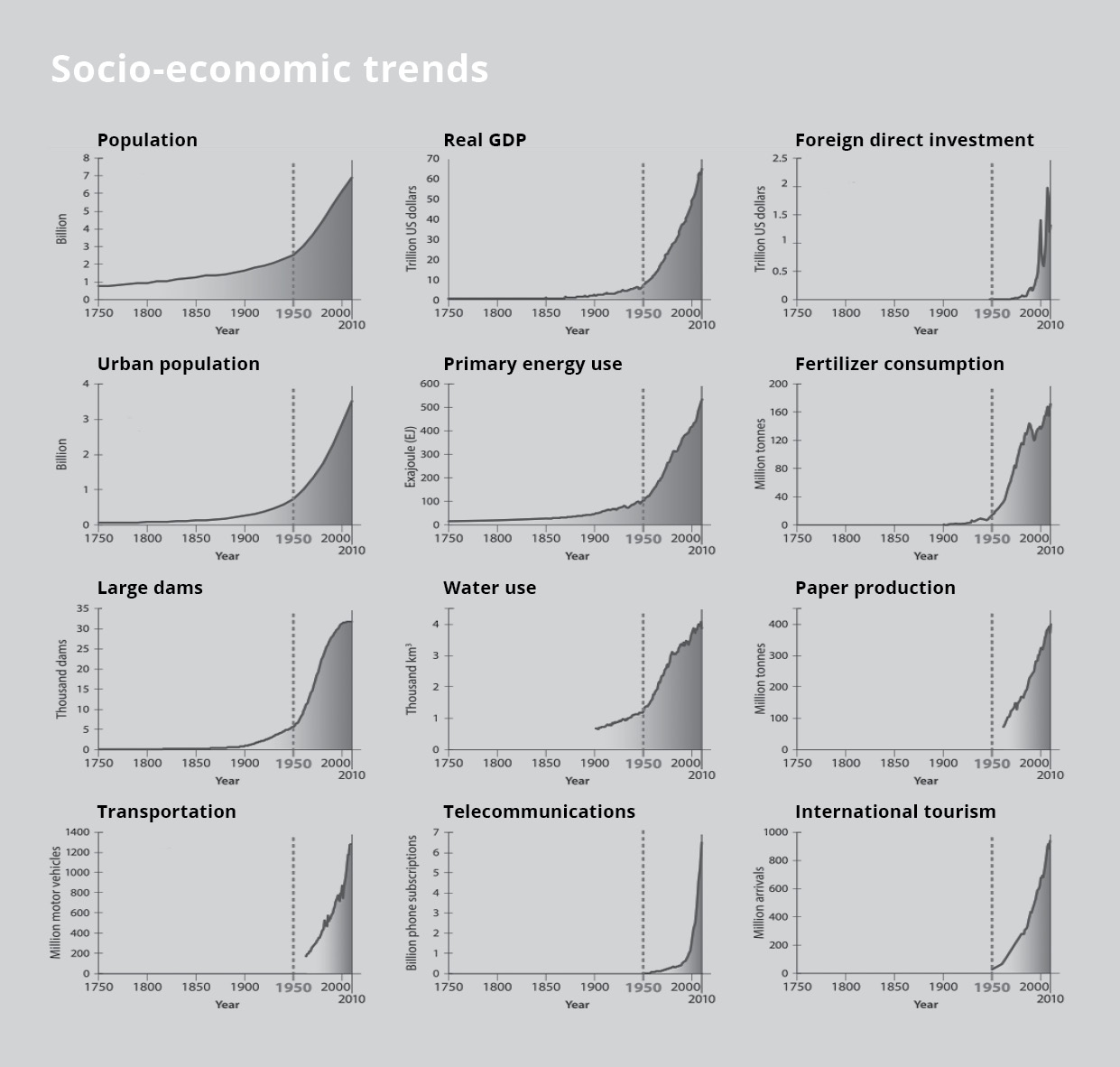
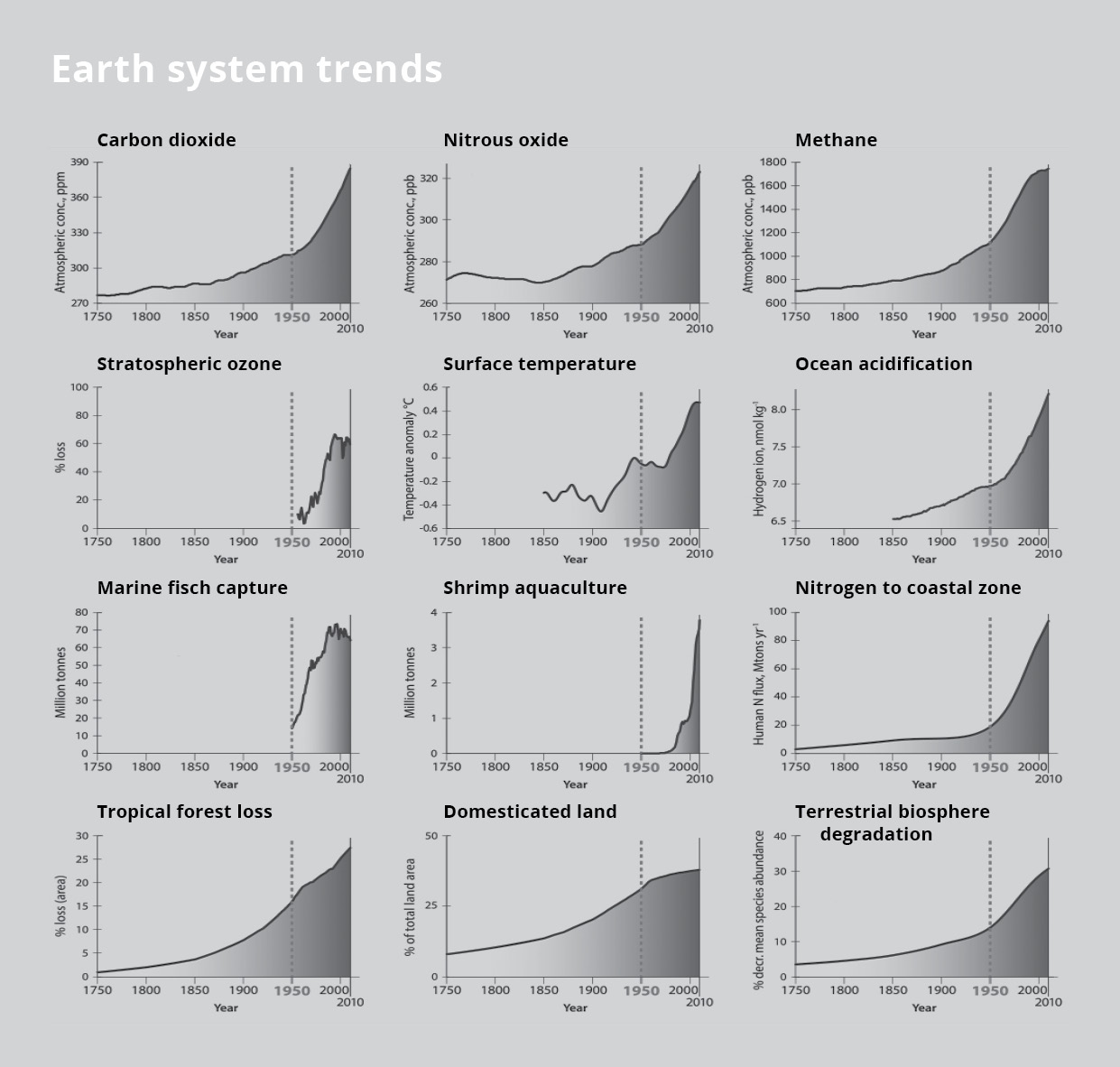
Figuur 2: Trends van het systeem Aarde en sociaaleconomische trends wijzen allemaal dezelfde kant op.
Wie denkt ‘de rente is bijna nul, er is nu geen groei’ zal bedrogen uitkomen.

.
Ook technologie is geen wondermiddel. Zoals we hierboven zagen, vormt het radicaal oprekken van de fles geen oplossing voor het probleem. Dat verschuift slechts het moment waarop de rekening gepresenteerd wordt – en ook maar voor even. Goed beschouwd is technologie een tweesnijdend zwaard. Enerzijds vergroot ze het potentieel van de middelen waarover een beschaving beschikt en dus ook haar vermogen om te blijven groeien. En anderzijds staat er precies om die reden dus ook meer op het spel. Want als voor elke verdubbeling een hoeveelheid grondstoffen nodig is die gelijk staat aan alle grondstoffen die de beschaving tot dan toe heeft verbruikt, dan zal ze ooit het punt bereiken dat het niet langer mogelijk is in de almaar toenemende grondstoffenvraag te voorzien.*
Er zijn nog twee redenen waarom beschavingen dikwijls een blinde vlek vertonen voor exponentiële groei en die hebben beide te maken met de menselijke psyche. De eerste is een overblijfsel van de oude steentijd, de tweede een meer recente verworvenheid (ook al wordt ook deze door datzelfde paleolithicum beïnvloed).
De menselijke geest is in wezen paleolithisch. Dat wil zeggen, evolutionair gezien is ze nog altijd ingesteld op het leven van de jager-verzamelaar op de Afrikaanse savannes. Dat was een leven dat was toegespitst op het dagelijks overleven in kleine groepen van intimi en stamverwanten. In de praktijk houdt dat in dat mensen uitblinken in concrete perceptie, maar veel minder goed bedreven zijn in abstractie. En dat ze volop oog hebben voor het onmiddellijke en het dramatische, maar sterk genegen zijn om lange-termijn-trends en hun gevolgen over het hoofd te zien. Om die reden zijn ze nadrukkelijk op het heden georiënteerd en kennen ze dikwijls minder waarde aan de toekomst toe of negeren ze die.
Het resultaat is dat het menselijke verstand, dat al niet bijzonder goed is toegerust op de cognitieve eisen van een geciviliseerd bestaan, het bij de omgang met de gevolgen van exponentiële groei al helemaal laat afweten.* Deze tekortkomingen verklaren ook waarom menselijke samenlevingen de neiging vertonen zich van de ene crisis naar de andere voort te slepen. Tegen de tijd dat de mens gemiddeld genomen doorheeft dat er een probleem is, is het al één minuut voor twaalf.
Maar zijn wij onze paleolithische wortels niet allang ontstegen door rationele wezens te worden? Ja, maar pas heel recent en slechts ten dele. Zo stellen we onze rationaliteit voornamelijk ten dienste van onze oerdriften – dat wil zeggen, in instrumentele zin, teneinde grootser te worden.
Bedenk eens waar we die blinde vlek vertonen? Bij het klimaat? Ons geldssysteem…?

.
Rationaliteit op zich biedt geen garantie voor een meer vooruitziende blik. Integendeel zelfs. Zo zal om het even welke econoom je maar al te graag uitleggen dat de ‘verdisconteerde waarde’ van de toekomst in feite nul bedraagt.
Uit het eerdere rentevoorbeeld blijkt waarom. Bij een rentevoet van 3,6 procent bedraagt de ‘huidige waarde’ van een euro van nu over honderd jaar slechts drie cent. Om die reden is alles wat ver in de toekomst ligt, praktisch gezien waardeloos. Zelfs gebeurtenissen die al over pakweg twintig jaar zullen plaatsvinden, worden door een ‘rationele’ homo economicus om die reden buiten beschouwing gelaten.
Hoewel de logica onweerlegbaar is, schuilt de denkfout in het begrip ‘huidige waarde’. Dat verraadt dat de econoom in diepste wezen nog altijd een holbewoner is. Het is het nu dat telt – niet volgend jaar, laat staan twintig of honderd jaar van nu. Dus jaagt de industriële beschaving haar voorraad fossiele brandstoffen er heel ‘rationeel’ zo snel mogelijk doorheen, terwijl even nadenken direct duidelijk maakt dat die in de toekomst veel waardevoller zal zijn.*
Bovendien, zelfs al bekruipt sommige mensen het gevoel dat iets niet helemaal in de haak is – dat de beschaving te groot, te complex en te problematisch is geworden om te managen – dan nog ontgaat hen wellicht dat exponentiële groei de voornaamste boosdoener is, en dat de oplossing dus gelegen is in het beheersen van die groei, niet in programma’s of technologieën die juist ontwikkeld zijn om verdere groei mogelijk te maken. Want zodra je een belemmering wegneemt, zorgt de hernieuwde groei ervoor dat de beschaving op ramkoers komt te liggen met de volgende en de daarop volgende belemmering, net zolang totdat ze onder de spanning bezwijkt.
Sommige mensen zullen tegenwerpen dat dit pessimisme ongegrond is. Het mag dan zo zijn dat voorgaande beschavingen met onoverkomelijke grenzen geconfronteerd zijn, zoiets kan echter onmogelijk opgaan voor de moderne, geïndustrialiseerde beschaving. Want wij zijn uniek in de zin dat we over machtige technologieën beschikken. Die technologieën stellen de mensheid in staat om de draagkracht van de aarde tot in het oneindige op te rekken en de consequenties van exponentiële groei voor altijd voor te blijven. Of zoals de futurist Herman Kahn claimde dat tegen het jaar 2200 ‘de mensheid overal rijk zal zijn en talrijk en de natuurkrachten zal beheersen.’* Met andere woorden, we kunnen de grootte van de fles nagenoeg zonder belemmeringen laten toenemen en zo Herman Kahns voorspelling in vervulling laten gaan.
Maar dat is een droom. We beschikken helemaal niet over de middelen om de beschaving almaar grootser te maken, want zelfs de machtigste technologie kan de natuurwetten niet negeren of omzeilen. Bovendien heeft technologie een schaduwzijde – ze vernietigt meer dan ze schept. Om te begrijpen waarom, gaan we in de inleiding bij de rubriek energie in op de derde biofysische barrière waarmee beschavingen te maken hebben: de wet van entropie.
We zien exponentiële groei in alle wereldtrends.
“De grootste tekortkoming van de menselijke soort is ons onvermogen om de exponentiële functie te begrijpen.”
Albert A. Bartlett*
Gerelateerd
Ecologie:
Ecologische uitputting
Energie:
Opgevoerde entropie
Complexiteit:
Tomeloze complexiteit
Ontwrichting:
Na de apocalyps
Eindeloze samengestelde groei


