Onze complexe wereld
Steve Keen*

Drie van de meest complexe systemen die we kennen zijn het menselijk brein, dat je in staat stelt om dit artikel te lezen; de economie, die het onderwerp is van dit artikel; en de biosfeer, waarin zowel ons brein als onze economie zijn geëvolueerd.
Deze systemen worden complex genoemd. Dat is niet omdat ze ingewikkeld zijn – al zijn ze dat natuurlijk wel –, maar omdat ze op complexe manieren op elkaar en op zichzelf inwerken. Noch ons heden noch ons verleden, laat staan onze toekomst kan worden begrepen zonder de terugkoppelingen te onderkennen die tussen elk van deze systemen én binnen elk van deze systemen bestaan.
Momenteel bereiken de interacties tussen deze systemen koortsachtige temperaturen. Covid-19 herinnert ons eraan dat we deel uitmaken van de biosfeer en er niet buiten of boven staan. De pandemie heeft onze economieën een gevoelige slag toegebracht, maar de aard en de omvang van de schade zijn verergerd door de manier waarop wij er als beschaving mee om zijn gegaan. Zo viel de pandemie in september 2020 niet alleen samen met de verschrikkelijke bosbranden in een groot deel van het westen van de Verenigde Staten, maar ook met een reeks ernstige overstromingen in het zuiden als gevolg van het historisch gezien grote aantal orkanen. Dit samenvallen verergerde beide problemen, want om de verspreiding van Covid-19 tot een minimum te beperken, moesten mensen geïsoleerd worden, terwijl de reddingsacties tot massale evacuaties noopten, waarbij mensen in noodvoorzieningen moesten worden ondergebracht. De ene crisis verergerde de andere.*
Economen hebben getracht om terugkoppelingseffecten in te kaderen middels het concept van evenwicht. Een evenwichtstoestand is een toestand waarin de belangrijkste variabelen van het systeem niet veranderen. Economen – zelfs een enkele niet-neoklassieke – stellen echter dat deze rusttoestand ‘de factor tijd niet “negeert”’ en dat in deze toestand ‘veranderingen juist voldoende tijd krijgen […] om hun volle effect te sorteren.’* De conventionele economische theorie heeft in feite de makkelijkste weg genomen door het evenwicht van het economisch systeem als uitgangspunt te nemen, in plaats van zich zorgen te maken om wat zij zelf als de kortstondige dynamiek bij het naderen van het evenwicht ziet.
Met andere woorden, men gaat ervan uit dat elk cyclisch proces uiteindelijk naar een rusttoestand tendeert en dat terugkoppelingen de schommelingen mettertijd altijd zullen dempen.

Een eeuw geleden toonde de wiskundige Alfred Lotka aan dat deze veronderstelling onjuist is, toen hij de dynamiek van twee op elkaar inwerkende soorten analyseerde – een roofdier en zijn prooi. In zijn voorbeeld was gras de ‘prooi’ en waren koeien de ‘roofdieren’.
Begin je met een klein aantal koeien in een wei, dan zal de hoeveelheid gras toenemen, omdat er niet genoeg koeien zijn om al het nieuwe gras op te eten. Voor koeien schept dit ideale omstandigheden om zich voort te planten, dus zal het aantal koeien toenemen. Een toenemend aantal koeien zal het gras uiteindelijk sneller opeten dan het groeit, waardoor de wei kaal begint te worden. Is deze fase eenmaal aangebroken, dan is er niet genoeg voer voor alle koeien om te overleven, zodat sommige van de honger zullen omkomen, en zijn we weer terug bij af. Figuur 1 toont dit als een cyclisch proces.
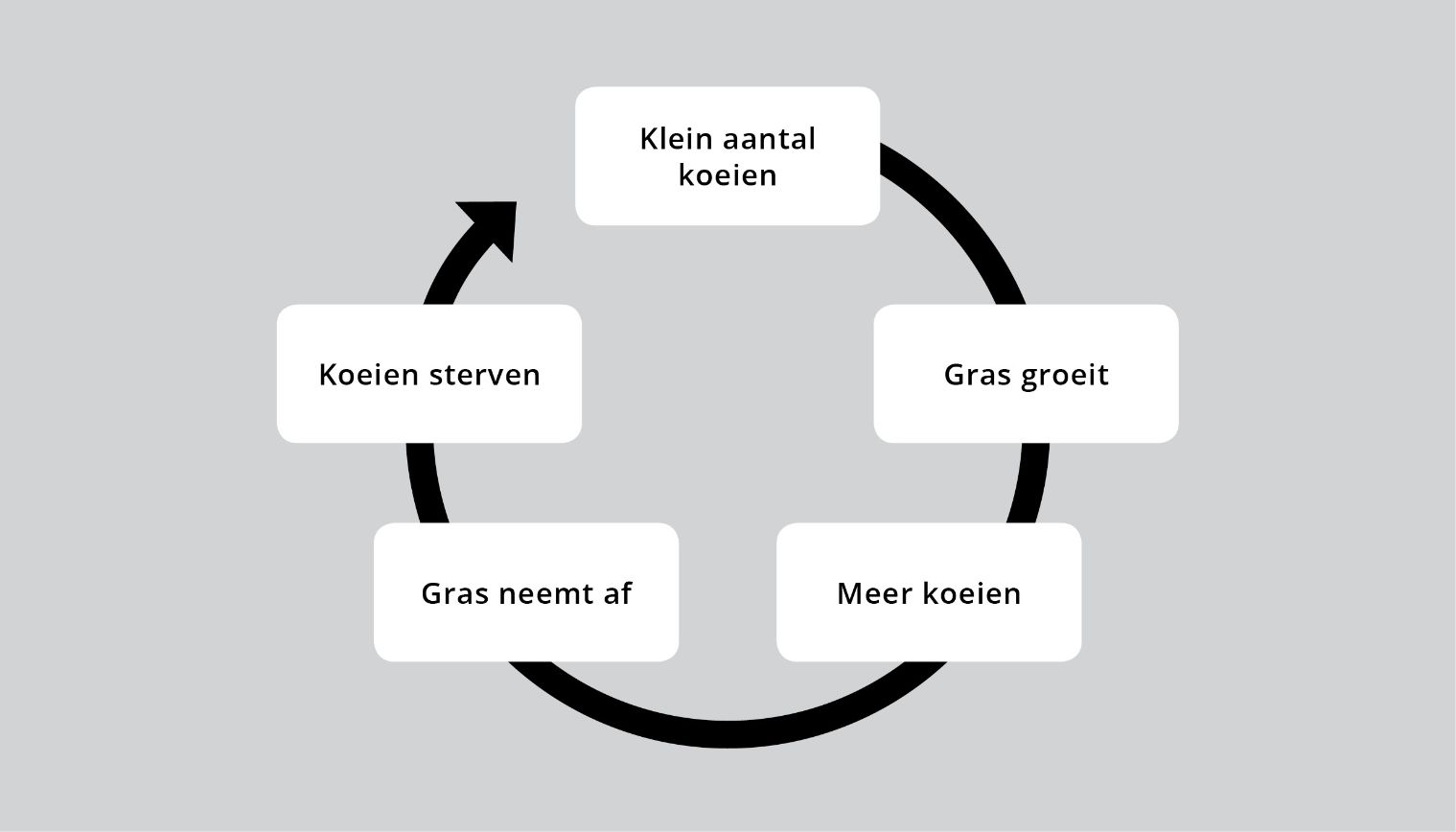
Figuur 1: De cyclische interactie tussen gras en koeien.
Mettertijd, zo verwachtte Lotka, zou dit tot afvlakkende cycli leiden, waarbij het aantal koeien en de hoeveelheid gras uiteindelijk naar evenwichtswaarden convergeren. Tot zijn verbazing ontdekte hij echter dat de hoeveelheid gras en het aantal koeien tot in het oneindige bleven schommelen:
‘Het was dan ook met grote verbazing dat de schrijver, toen hij zijn methode op bepaalde speciale gevallen toepaste, ontdekte dat deze tot ongedempte, en dus oneindig voortdurende, oscillaties leidden.’*
Lotka’s ontdekking was de geboorte van wat nu bekend staat als complexe systeemanalyse. Een essentieel aspect van deze benadering is dat je niet kunt doen wat conventionele economen doen: je kunt evenwicht niet als een gemakkelijke uitweg gebruiken. Bij de meeste complexe systemen vertelt het evenwicht je niet waar het systeem uiteindelijk zal uitkomen, maar waar het systeem nooit zal zijn.
In plaats van naar een evenwicht te convergeren, hebben complexe systemen de neiging om oneindig te oscilleren – zoals Lotka in zijn model van koeien en gras ontdekte.

De dynamiek van het roofdier-prooimodel, zoals Lotka’s ontdekking werd genoemd, wordt getoond in figuur 2, niet met koeien en gras maar met haaien en vissen als voorbeeld. Het model heeft een evenwicht,1 weergegeven door de lijnen in de tijdplots en de stip in de faseplots, maar het is ‘neutraal’: als het model vanuit een evenwichtstoestand begint, zal het er nooit naar terug convergeren, maar het zal er ook niet verder van verwijderd raken.
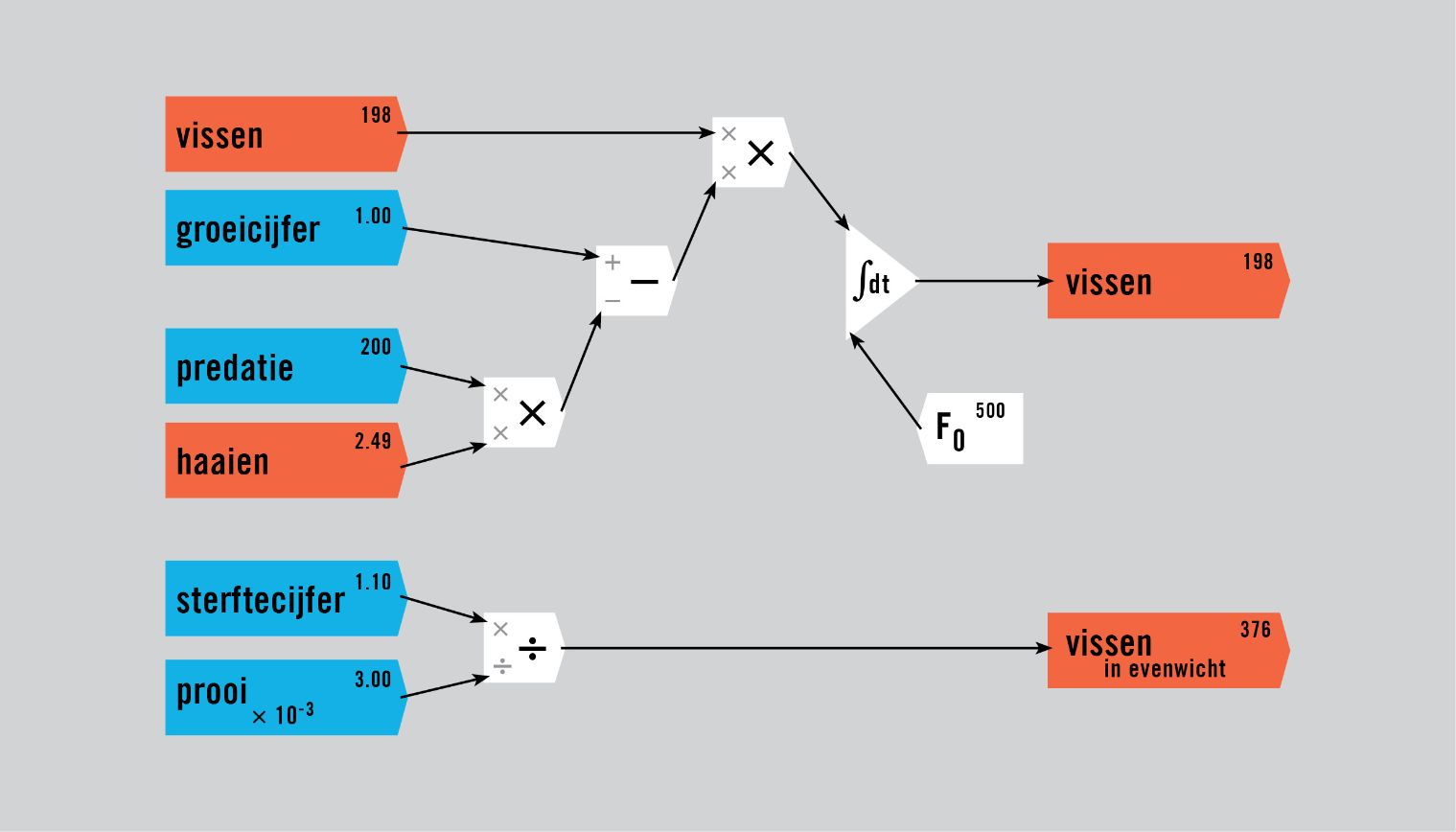
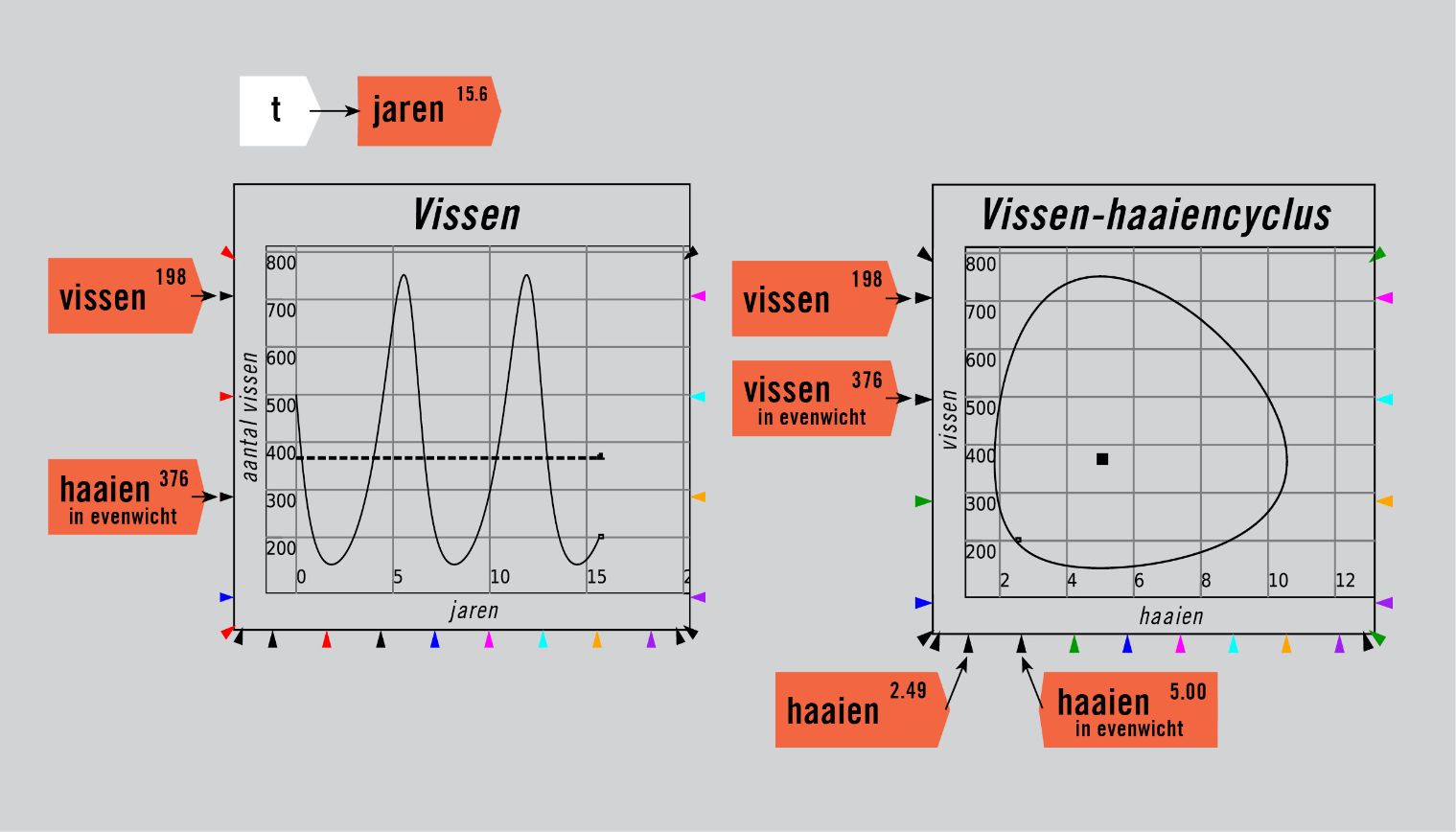
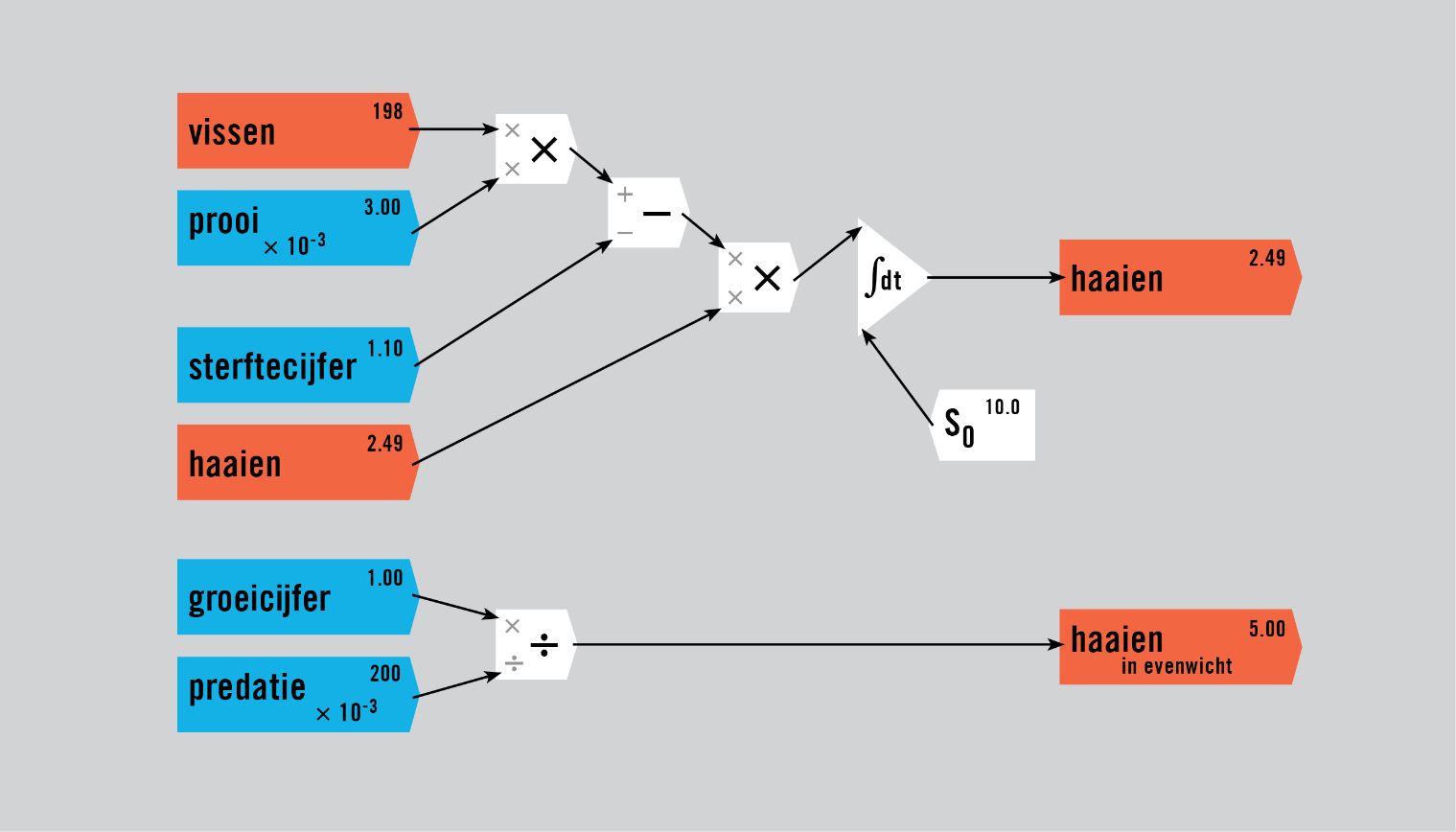
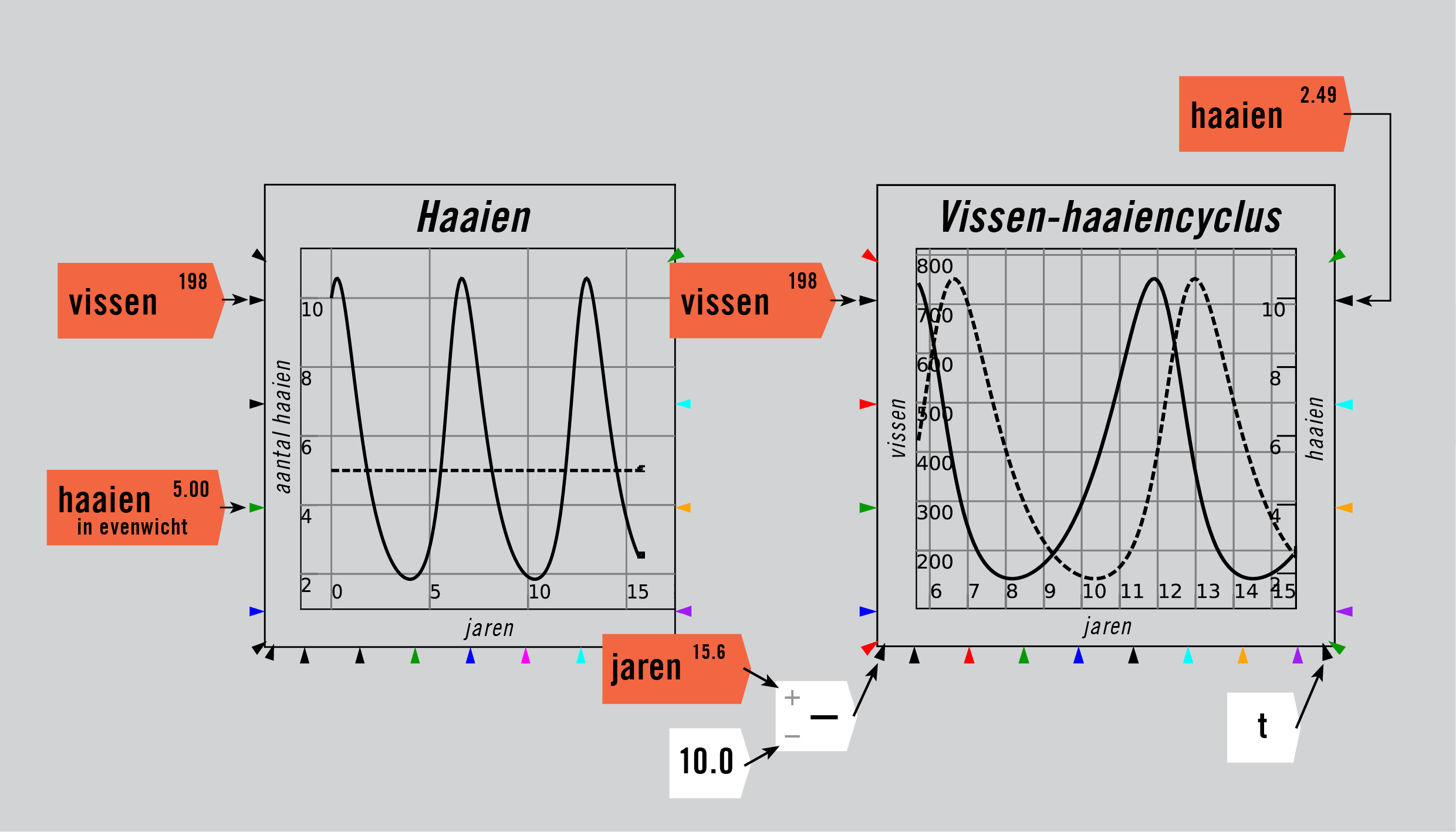
Figuur 2: Een roofdier-prooimodel in Minsky met haaien en vissen.
Een beperking van Lotka’s model was dat de oscillaties altijd van dezelfde grootte en frequentie waren, wat niet overeenkomt met wat we in de echte wereld waarnemen. In echt bestaande systemen zijn cycli net als de economie aperiodiek: er zijn hausses en baisses, maar de omvang en frequentie van elke hausse en elke baisse is verschillend van die van de vorige. De meeste van het kleine aantal economen dat überhaupt van Lotka’s ontdekking op de hoogte was, negeerden die om deze reden. De dominante verklaring in de economie voor cycli werd dat zij het resultaat waren van externe (‘exogene’) schokken die een anderszins stabiel systeem verstoorden. Een decennium na de ontdekking van Lotka verwoordde Ragnar Frisch, oprichter en hoofdredacteur van het tijdschrift Econometrica, het als volgt:
‘Het merendeel van de economische schommelingen die we tegenkomen lijken het meest plausibel verklaard te kunnen worden als vrije schommelingen. Naar het zich laat aanzien worden zij veroorzaakt door het feit dat bepaalde impulsen het economisch mechanisme van buitenaf treffen, waardoor min of meer regelmatige oscillaties in gang worden gezet. […]
‘[D]e energiebron die de economische cycli in stand houdt, bestaat uit grillige schokken […] Nieuwe innovaties en exploitaties maken met onregelmatige tussenpozen hun opwachting […] deze onregelmatige schokken kunnen min of meer regelmatige cyclische bewegingen veroorzaken […] Als je met een stok op een houten hobbelpaard slaat, zal de beweging van het paard een hele andere zijn dan die van de stok.’ *
Deze opvatting van Frisch zou drie decennia later echter ontkracht worden met de ontdekking van de chaostheorie, zoals in de volgende aflevering duidelijk wordt.

Deze verwerping door economen van de stelling uit de complexe systeemanalyse dat economische cycli endogeen zijn – veroorzaakt door de dynamiek binnen de economie zelf, in plaats van door schokken van buitenaf – werd drie decennia later ontkracht door de ontdekking van wat enige tijd ‘chaotische dynamiek’ in weersystemen werd genoemd. Deze ontdekking werd voor het eerst uit de doeken gedaan in een artikel met de veelzeggende titel ‘Aperiodic Deterministic Flow’. *
In die tijd gebruikten meteorologen lineaire modellen voor hun weersvoorspellingen. Edward Lorenz was hier niet tevreden mee, omdat het ene aspect van het weer, bijvoorbeeld de luchttemperatuur, een niet-lineaire invloed had op een ander aspect, zeg de windsnelheid. Veranderingen in luchttemperatuur resulteerden namelijk niet in een lineaire toename van de windsterkte, maar in een verveelvoudiging ervan. Ter illustratie bouwde hij een uiterst gecompliceerd vloeistofdynamica-model om tot een eenvoudig model met slechts drie variabelen (x, y en z) en drie constanten (a, b en c).
Oppervlakkig gezien was dit model slechts iets gecompliceerder dan dat van Lotka, dat twee variabelen en vier constanten telde, maar in de praktijk gedroeg Lorenz’ model gedroeg zich totaal anders. Het genereerde cycli die zowel qua amplitude als frequentie niet alleen sterk van die Lotka afweken, maar aanvankelijk ook volkomen chaotisch leken. Dat wil zeggen, totdat Lorenz tot de ontdekking kwam dat onder de ogenschijnlijk ‘chaotische’ bewegingen van de variabelen x, y en z na verloop van tijd het schitterende patroon van x of y uitgezet tegen z opdoemde, dat hij het ‘vlindereffect’ doopte – zie figuur 3.
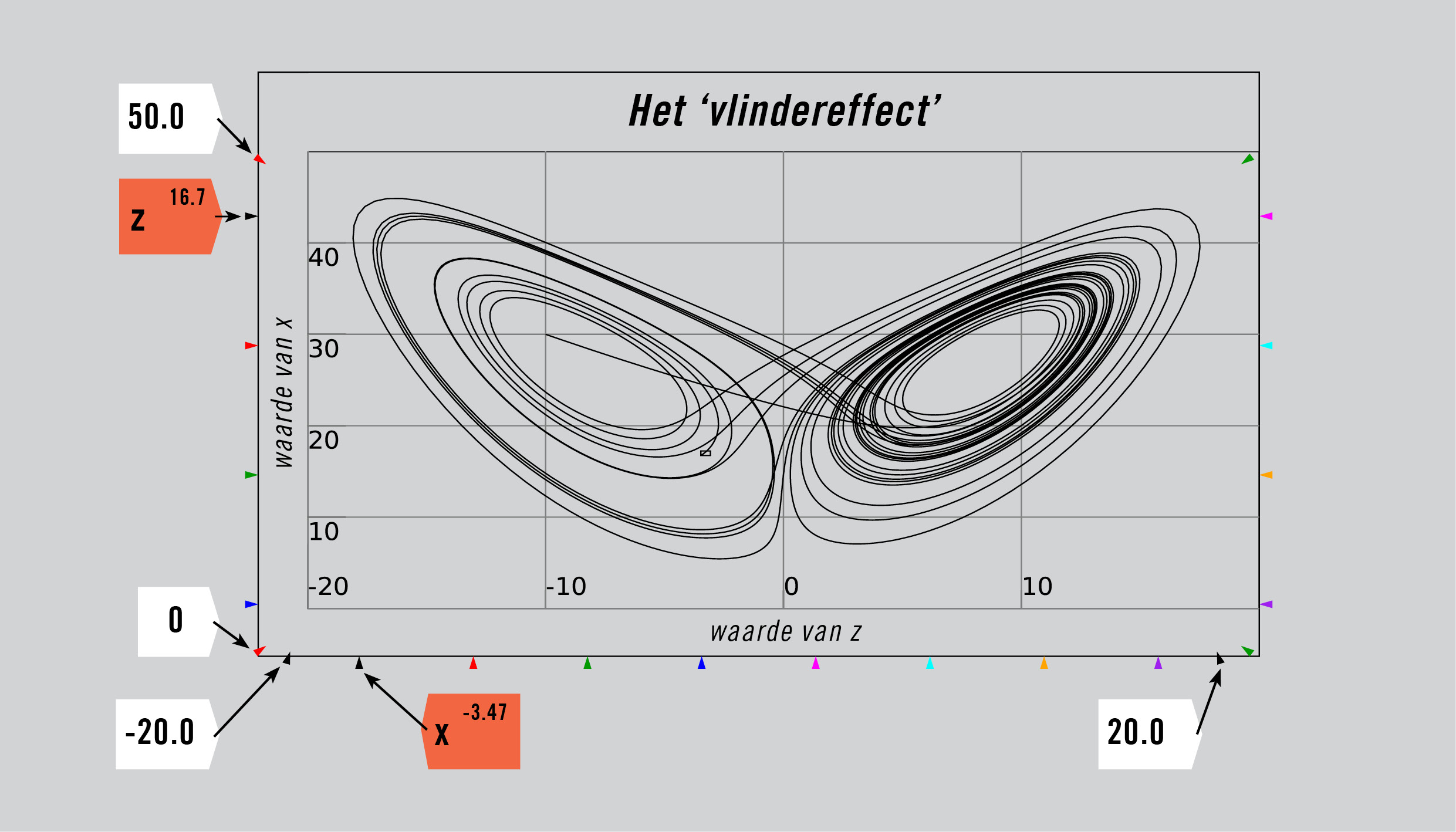
Figuur 3: Lorenz’ model van aperiodieke weercycli.
Zoals we zullen zien verrijkte Lorenz’ model de wereld met een nieuw type evenwicht, dat van de ‘vreemde aantrekker’.

Het artikel van Lorenz liet de wereld kennismaken met een heel nieuw soort evenwicht, dat van de ‘vreemde aantrekker’. Dit is een evenwicht dat het systeem vanaf enige afstand benadert, maar waarvan het wordt afgestoten zodra het dichterbij komt. In Lorenz’ model zitten twee vreemde aantrekkers, die zich in de lege ruimten tussen de twee vlindervleugels bevinden (zie figuur 3 in de vorige aflevering). Het model kent drie evenwichten, die bij realistische parameterwaarden alle drie onstabiel zijn.
Dit gedrag wordt veroorzaakt doordat drie of meer systeemvariabelen op niet-lineaire wijze op elkaar inwerken. Zowel het model van Lotka als dat van Lorenz kennen niet-lineaire termen – termen waarbij de ene variabele met een andere vermenigvuldigd wordt. Lotka’s model bracht periodieke cycli van een vaste grootte voort omdat het slechts twee soorten (roofdieren en prooidieren) telde – hoewel er gemakkelijk meer kunnen worden toegevoegd. De drie variabelen in het model van Lorenz bleken het minimale aantal dat nodig was om aperiodieke cycli te genereren, zoals we die in de echte wereld zien.*
Waarom een dynamisch systeem met drie variabelen zo sterk verschilt van een systeem met twee variabelen is een kwestie van meetkunde: een van de regels van differentiaalvergelijkingen is dat als je de waarden van de variabelen van een systeem in één simulatie tegen elkaar uitzet, de paden elkaar niet kunnen kruisen. Zet je in een systeem met twee variabelen de ene variabele tegen de andere uit, dan levert dat een tweedimensionale vorm op – ongeveer zoals een tekening op een tafelblad, waarbij je nooit je vinger van de tafel hoeft op te tillen en je nooit je pad kruist.
Dit laat je slechts vijf opties: een inwaartse spiraal waarbij je uiteindelijk een punt bereikt; een uitwaartse spiraal waarvoor je almaar meer tafelbladen nodig hebt; een inwaartse spiraal die naar een kromme convergeert (zoals een cirkel), zonder die ooit echt te bereiken; een uitwaartse spiraal waarbij je eveneens naar een cirkel convergeert; of, als vijfde, voor altijd op een gesloten pad te blijven – dat wil zeggen, precies hetzelfde patroon te blijven herhalen zonder het ooit te doorsnijden.2
Drie variabelen levert je een driedimensionale vorm op – een doos bijvoorbeeld. Herhaal nu hetzelfde proces in je denkbeeldige doos op het tafelblad. Dan zie je dat je gemakkelijk ingewikkelde vormen kunt tekenen, zoals de vlinder van Lorenz, zonder ooit je pad te kruisen.
In de volgende aflevering zien we hoe de ontdekking van Lorenz niet alleen de meteorologie, maar ook het economisch denken – in zeer geringe mate, weliswaar – heeft beïnvloed.

Lorenz’ ontdekking leidde tot een omwenteling in de meteorologie. Een van de belangrijkste redenen dat weersvoorspellingen tegenwoordig zoveel nauwkeuriger zijn dan een halve eeuw geleden – zelfs nu de klimaatverandering het weer steeds meer in de war schopt – is dat meteorologen Lorenz’ advies opvolgden en grootschalige, niet-lineaire modellen van de atmosfeer begonnen te bouwen. Zijn ontdekking heeft ook de meeste andere natuurwetenschappen sterk beïnvloed.
Maar de doorsnee economen, vertegenwoordigers van een notoir insulaire sociale wetenschap,* negeerden Lorenz grotendeels. Hoewel een handvol economen, waaronder ikzelf, de resultaten van Lorenz wel ter harte namen, ging de overgrote meerderheid door met Frisch’ ondeugdelijke benadering van de economie als een stabiel systeem, waarin de schommelingen door ‘exogene schokken’ veroorzaakt worden.
Complexe systeemmodellen zijn dus in staat om aperiodieke cycli in een systeem te verklaren. De vraag is dus waarom economen, behalve uit onwetendheid, de economie niet als een complex systeem analyseren en zich op Frisch’ ongeldige raamwerk – van een stabiel systeem dat slechts onderworpen is aan exogene schokken – blijven verlaten?
De enige verdediging die je zou kunnen aanvoeren is dat de economie ’te complex’ is om haar in een staat van onbalans of met fundamenteel niet-lineaire componenten te modelleren. Er zijn vele eenvoudigere benaderingen denkbaar zodra je ervan uitgaat dat je niet-lineaire interacties in een systeem probleemloos kan negeren. Om te beginnen kan een niet-lineair systeem met drie of meer variabelen doorgaans niet analytisch worden opgelost. Bij lineaire modellen is dat meestal wel mogelijk. En in tegenstelling tot bij een niet-lineair model, is het ook veel gemakkelijker om een lineair model te schatten en het aan de gegevens aan te passen. Lineaire modellen, zelfs die met vele vergelijkingen, zijn inherent eenvoudiger dan zelfs de bescheidenste niet-lineaire modellen, en de drang om ‘het eenvoudig te houden’ zit in alle wetenschappen diep ingesleten.
Maar zoals Einstein vaak geparafraseerd wordt, draait het erom de dingen zo ‘eenvoudig mogelijk te houden, maar niet eenvoudiger’. Wat Einstein werkelijk zei was dat:
‘[…] het nauwelijks ontkend kan worden dat het hoogste doel van alle theorie is om de onherleidbare basiselementen zo eenvoudig en beperkt mogelijk te houden zonder de adequate weergave van een enkel ervaringsgegeven op te hoeven geven.’*
Dat het doorsnee economisch denken dit principe van Einstein schendt, wordt duidelijk in de volgende aflevering.

De beste illustratie dat de zeer ingewikkelde maar fundamenteel lineaire, stabiele-evenwichtsmodellen – waar doorsnee economen de voorkeur aan geven – dit principe van Einstein schenden, was dat ze faliekant tekortschoten bij het voorzien van de wereldwijde financiële crisis van 2007-2010. Zoals al eerder is opgemerkt,* moest 2008 volgens deze modellen juist een fantastisch jaar worden. De voorspellingen van het ‘dynamisch stochastisch algemeen evenwicht’-model van de OESO lagen aan de basis van de optimistische OESO-ramingen uit juni 2007. Twee maanden later brak de crisis uit.
Dat vormt het negatieve argument tegen lineaire modellen, en evenwichtsgerichte modellen in het bijzonder. Het positieve argument voor de niet-lineaire, complexe systeembenadering in het economisch denken is het feit dat de kernverschijnselen die de crisis hebben veroorzaakt, zichtbaar gemaakt kunnen worden met behulp van een zeer eenvoudig, fundamenteel niet-lineair, complex systeemmodel van de economie, dat ik voor het eerst in 1992 ontwikkeld heb.* De uitkomsten van dit model noopten me om vanaf december 2005 te waarschuwen dat er een crisis op til was.* Ondanks zijn eenvoud en gestileerde aard – of misschien wel daardoor, denk aan Lorenz’ weermodel in figuur 3 – gaf het de essentiële kenmerken van de reële economie in de aanloop naar de crisis weer:
– De omvang van de economische cycli nam af, een fenomeen dat door doorsnee ‘neoklassieke’ economen als een goede zaak werd gezien, en waarvoor toenmalig vicevoorzitter van de Amerikaanse centrale bank Ben Bernanke – namens de Federal Reserve en de neoklassieke economen die hierin dominant zijn – met de eer zou strijken;*
– De inkomensverdeling verschoof van arm (werknemers) naar rijk (bankiers), hetgeen economen wel waarnamen maar niet konden verklaren (en waar ze zich ook niet heel druk om maakten); en
– Het niveau van de particuliere schuld steeg ten opzichte van het bbp, hetgeen ze eveneens negeerden.
Ik heb dit model gebouwd om een vorm te kunnen geven aan de ideeën van een van de grote niet-neoklassieke economen, Hyman Minsky, naar wie het programma Minsky vernoemd is.

Hymen Minsky (1919-1996) ontwikkelde zijn theorie van systemische instabiliteit in het kapitalisme door een eenvoudige vraag te stellen: kan ‘Het’ – dat wil zeggen een Grote Depressie – opnieuw gebeuren? Teneinde deze vraag te beantwoorden stelde Minsky dat ‘het noodzakelijk is om een economische theorie te hebben die grote depressies tot één van de mogelijke toestanden maakt waarin ons type kapitalistische economie zich kan bevinden.’ * Zijn verbale model richtte zich op de tweeledige rol van particuliere schulden, die ertoe kunnen leiden dat de investeringen hoger uitkomen dan de winsten én dat ze het investeringsniveau omlaag kunnen trekken wanneer de schuld te hoog is in verhouding tot het inkomen. Hij formuleerde het als volgt:
‘Het natuurlijke uitgangspunt voor het analyseren van de relatie tussen schuld en inkomen is een economie met een cyclisch verleden die nu goede prestaties levert […] Naarmate de periode waarin de economie het goed doet langer voortduurt, worden er in directiekamers twee dingen duidelijk. Bestaande schulden worden gemakkelijk bekrachtigd en afdelingen die voorheen zwaar in de schulden zaten, gedijen […] Het gevolg is dat gedurende een periode waarin de economie het goed doet, de opvattingen over een aanvaardbare schuldenstructuur veranderen […] Duurt dit langer voort dan verandert de economie in een hoogconjunctuur.
‘Stabiele groei is onverenigbaar met de wijze waarop investeringen worden bepaald in een economie van met schuld gefinancierde eigendom van kapitaalgoederen, en de mate waarin een dergelijke schuldfinanciering kan worden afgelost, wordt bepaald door de markt. Hieruit volgt dat de fundamentele instabiliteit van een kapitalistische economie opwaarts gericht is. De neiging om goede economische prestaties om te zetten in een speculatieve investeringsgolf vormt de fundamentele instabiliteit in een kapitalistische economie.‘*
Het fundamentele causale proces dat Minsky voor ogen had was dat:
– In de nasleep van een recessie zowel bedrijven als banken terughoudend zijn bij het aangaan van schulden. Daarom ontvangen alleen conservatief ingeschatte projecten financiering;
– Door deze conservatieve hefboomwerking de meeste projecten slagen – wat ertoe leidt dat bedrijven en banken avontuurlijker worden;
– Extra leningen meer investeringen financieren, waardoor de economie bloeit, maar ook de particuliere schuld toeneemt;
– De hausse de lonen en grondstoffenprijzen opdrijft, waardoor de winsten op het hoogtepunt van de boom dalen;
– De investeringen teruglopen, en de economie in een nieuwe recessie terechtkomt;
– De lonen en grondstoffenprijzen dalen, waardoor de winstgevendheid zich herstelt, maar met een hogere schuldenlast dan voorheen; en
– De cyclus zich net zolang herhaalt totdat de schuld uiteindelijk zo hoog is dat de rente op de schuld hoger is dan de winst en de economie in een Grote Depressie belandt.
In mijn Minsky-programma heb ik deze uitspraken omgevormd tot een causaal model.

Dit proces kan in een uiterst eenvoudige causale keten gevangen worden:
1. Kapitaal bepaalt Output;3
2. Output bepaalt Werkgelegenheid;
3. De werkgelegenheidsgraad bepaalt de verandering van de loontarieven;
4. De Output minus de Lonen en de rentebetalingen bepaalt de winst;
5. De winstvoet bepaalt het niveau van de investeringen,4 hetgeen overeenkomt met de verandering in Kapitaal – wat ons weer terugbrengt naar het startpunt van deze causale keten; en
6. Het verschil tussen investering en winst bepaalt de verandering in de (particuliere) schuld.
Met Minsky of om het even welk ander op de systeemdynamica geënt programma kunnen we deze stapsgewijze verbale keten in een wiskundig model omzetten. Hoewel deze verbale keten geen veronderstellingen bevat over cycli of de inkomensverdeling, komen de reële verschijnselen van stijgende schulden, aanvankelijk afnemende en vervolgens toenemende cycli, en een verschuivende inkomensverdeling van arm (werknemers) naar rijk (bankiers) in een simulatie van dit model verrassend genoeg allemaal naar voren – zie figuur 4.
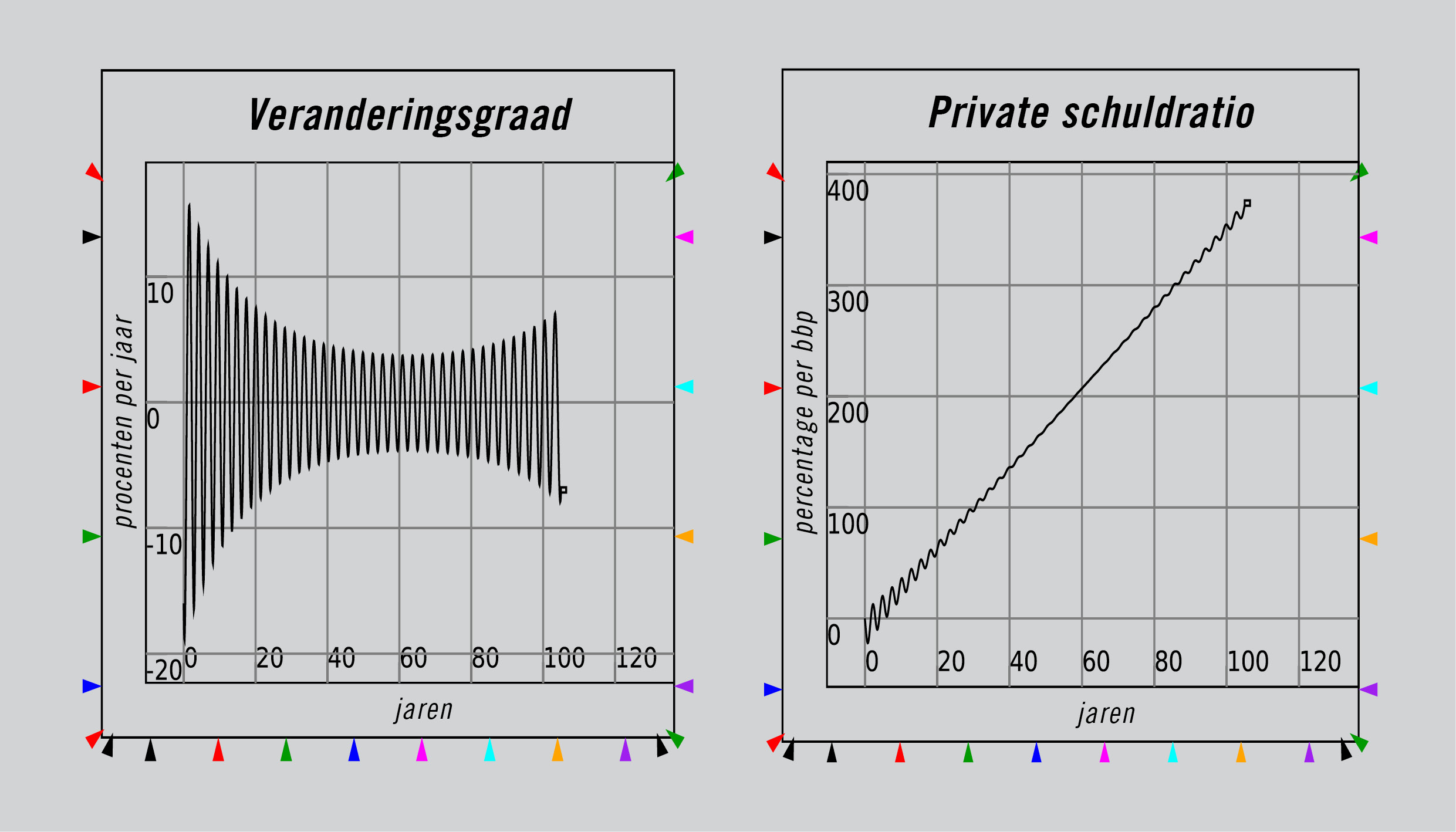
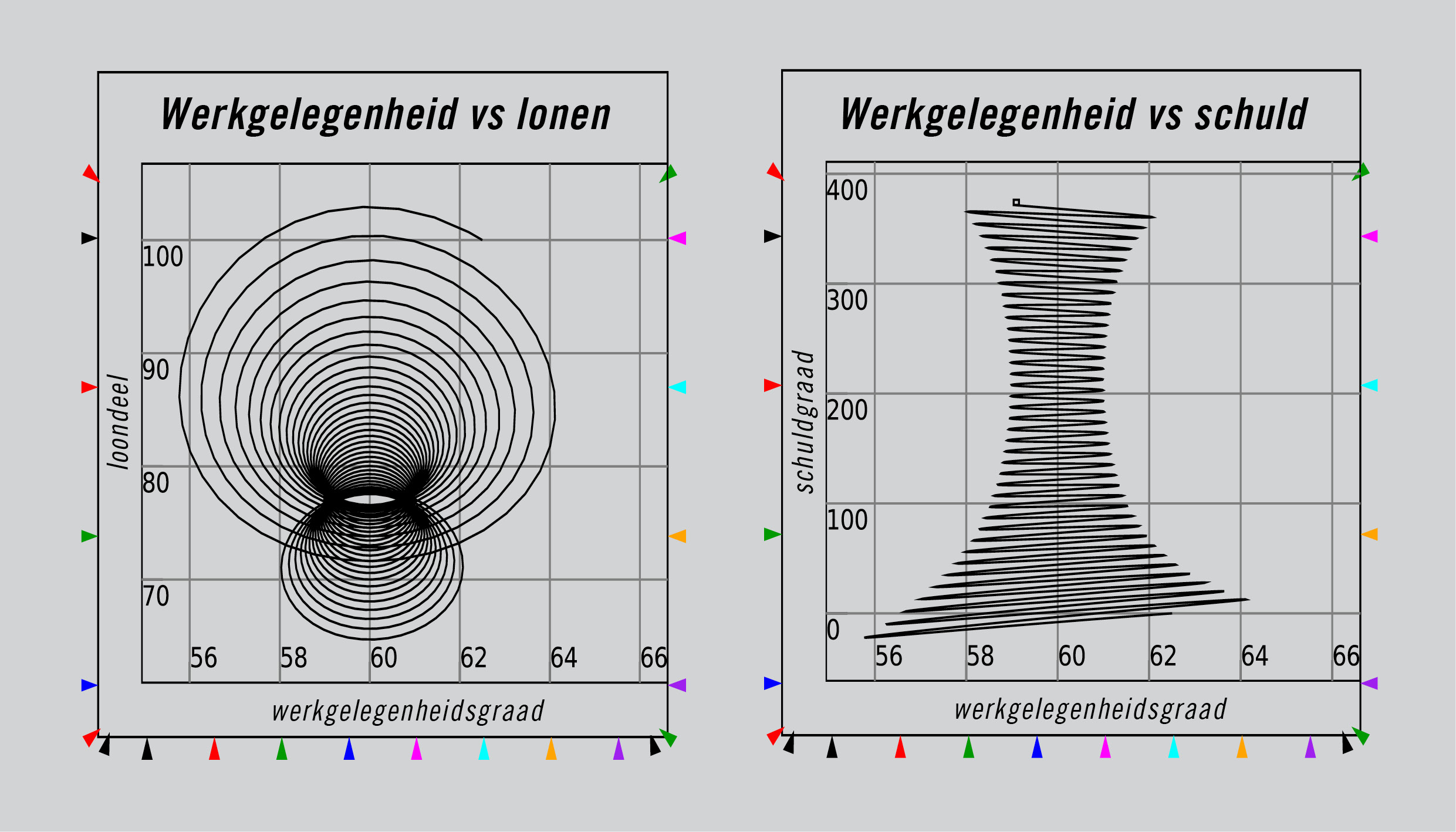
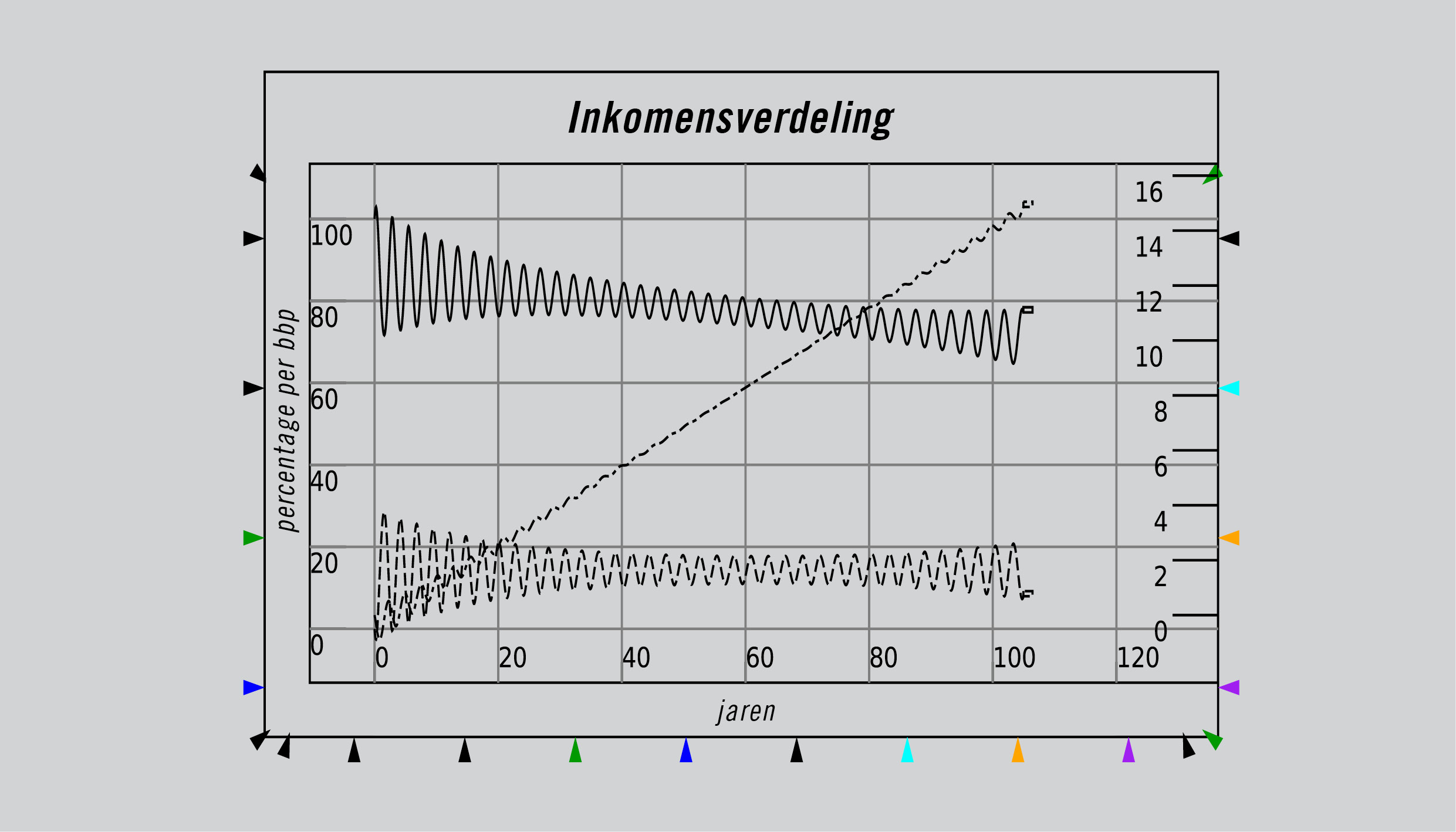
Figuur 4: Het Keen-Minsky model en de ‘Intermitterende Route naar Chaos’.
Wat je hier ziet is een voorbeeld van een veel voorkomend verschijnsel in complexe systeemmodellen, dat van ‘emergente eigenschappen’. Dat zijn eigenschappen die het model vertoont, maar die niet middels aannames of formules in het model zijn ingebouwd.
In plaats daarvan ‘emergeren‘ ze uit de interacties tussen de systeemvariabelen: in dit geval tussen de werkgelegenheidsgraad, het loonaandeel van het bbp en het niveau van de particuliere schuld in verhouding tot het bbp.

De twee belangrijkste eigenschappen van dit model zijn dat:
– Hoewel de werknemers in dit eenvoudige model niet lenen, zij wel degenen zijn die effectief voor de hogere schuld betalen, via een daling van hun loonaandeel in het bbp, terwijl het aandeel van de kapitalisten constant blijft. De ongelijkheid neemt toe omdat de inkomensgroei van het aandeel van de (relatief rijke) bankiers evenredig is aan de afname van het aandeel van de (relatief arme) werknemers; en
– De cycli afnemen en lijken te verdwijnen, om later terug te keren om steeds extremere vormen aan te nemen.
Wat zijn de oorzaken van deze twee emergente eigenschappen – het feit dat de werknemers en niet de bedrijven uiteindelijk voor de hogere schuldenlast opdraaien alsmede het verschijnsel van afvlakkende en vervolgens aanzwellende cycli?
De eerste eigenschap doet zich voor omdat dit model wordt voortgedreven door het verlangen van kapitalisten om te investeren, zoals blijkt uit de investeringsvergelijking, waarin de winstvoet het aandeel van de investeringen in het totale bbp bepaalt. Dit impliceert dat er een bepaalde winstvoet bestaat waarbij de investeringen precies gelijk zijn aan de winst: in de simulaties hier is dat een winstvoet van 4,3 procent, oftewel een aandeel van 12,9 procent van het bbp dat naar de kapitalisten gaat. Dan blijft er 87,1 procent van het bbp over voor verdeling tussen werknemers en bankiers, en het maakt de kapitalisten niet uit hoe dat tussen hen verdeeld wordt. De dynamiek van het model stuwt meer inkomen richting de bankiers en weg van de werknemers.
De werkgelegenheid neemt toe naarmate de economie aantrekt als gevolg van hogere investeringen. Als gevolg hiervan stijgt de werkgelegenheidsgraad substantieel, hetgeen de lonen opdrijft. Aangezien de investeringen die de winsten overschrijden met schulden worden gefinancierd, stijgt de schuldgraad ook tijdens de hoogconjunctuur, zodat ook de kosten van de schuldendienst stijgen. Deze stijgende loon- en rentekosten betekenen uiteindelijk dat de winsten die de kapitalisten bij het begin van de hoogconjunctuur verwacht hadden, niet worden gerealiseerd. Doordat een groter deel van de output naar werknemers en bankiers gaat, is de winst voor de kapitalisten geringer dan verwacht. De investeringen lopen terug, de economie groeit minder snel en de hoogconjunctuur maakt plaats voor een baisse.
De neergang maakt een eind aan de dynamiek die door de hausse in gang is gezet, maar doet het effect van de hausse op de particuliere schuld niet volledig teniet. De totale vraag daalt, wat leidt tot een daling van de werkgelegenheid en van de lonen; tegelijkertijd echter leiden de teruglopende kasstromen er na de crisis toe dat de schuldaflossing bij de geplande betalingen achterblijft. Hierdoor blijft er in de herstelfase na de crisis dus een restant van onbetaalde schuld achter.
Uiteindelijk keert het winstaandeel van de productie terug naar een niveau dat een nieuwe periode van euforische verwachtingen en hoge, met schuld gefinancierde investeringen inluidt, zij het dit keer bij een hoger schuldniveau in verhouding tot het bbp dan bij de vorige hausse.
Bij een hoger schuldniveau gaat een groter deel van het inkomen naar de bankiers en blijft er voor de werknemers een kleiner deel over. De werknemers betalen dus de prijs voor het hogere schuldniveau in termen van een lager loonaandeel in het bbp, ook al lenen zij zelf niet.
In de taal van wiskundigen heet deze tweede emergente eigenschap – dat cycli afvlakken en vervolgens aanzwellen naarmate de crisis nadert – de 'intermitterende route naar chaos'. Dit verschijnsel werd voor het eerst ontdekt in de vloeistofdynamica* bij de analyse van Lorenz' weermodel, dat eerder al ter sprake kwam. Het kan alleen volledig in wiskundige termen worden uitgelegd, maar ik zal mijn best doen om het hieronder in woorden te beschrijven. Heb je geen wiskundige achtergrond, dan is dit misschien een goed moment om een koffiepauze in te lassen.
Een cruciaal onderdeel van het verschijnsel van complex of 'chaotisch' gedrag is gelegen in de 'niet-lineariteit' van het model. Aangezien het model termen bevat waarbij de ene systeemtoestand met de andere wordt vermenigvuldigd – zeg, de schuldgraad vermenigvuldigd met het aandeel van de werknemers in het bbp – maakt het voor het effect van deze interactie een groot verschil uit of het model ver van een evenwichtstoestand verwijderd is of dat het zich juist dicht bij een evenwicht bevindt. Ver verwijderd van de evenwichtstoestand (ook wel 'ver van evenwicht' genoemd), is het product van het verschil van elk van deze variabelen ten opzichte van hun evenwichtswaarden zeer groot: onder bepaalde omstandigheden kan dit het systeem terug in de richting van het evenwicht duwen. Maar zodra deze variabelen de evenwichtstoestand naderen (ook wel 'dicht bij evenwicht'), neemt de grootte van dit product zeer snel af – net zoals x tot de tweede macht veel groter is dan x wanneer x groter is dan 1, maar veel kleiner dan x wanneer x kleiner is dan 1: het kwadraat van x is 4 wanneer x 2 is, maar ¼ wanneer x ½ is. Ver van evenwicht hebben de niet-lineaire termen in een model dus de overhand over de lineaire termen, terwijl dicht bij evenwicht de lineaire termen de overhand hebben over de niet-lineaire termen.
Nogal paradoxaal houdt dit in dat waar de niet-lineaire termen ervoor zorgen dat een niet-lineair model zich ver van evenwicht heel anders gedraagt, de lineaire termen de stabiliteit van een evenwicht bepalen.
Om deze reden verschilt het gedrag van een niet-lineair model sterk van de fundamenteel lineaire modellen die de neoklassieke economen gewoonlijk bouwen: als het evenwicht in een lineair model een 'afstoter' is – als die het systeem wegduwt in plaats van naar zich toe te trekken – dan stoot die zowel ver van evenwicht als dicht bij evenwicht af. Dat zal onvermijdelijk betekenen dat het model buiten zijn zinnige grenzen wordt geduwd: je krijgt dan negatieve hoeveelheden goederen, of negatieve prijzen, die in een economisch model volkomen betekenisloos zijn.
Maar in een niet-lineair model kan het gedrag dicht bij evenwicht sterk verschillen van het gedrag ver daarvandaan. Als het evenwicht 'dicht bij' – daar waar de lineaire termen de overhand hebben – als een afstoter functioneert, dan kan dat evenwicht 'ver weg' – daar waar de niet-lineaire termen de baas zijn – ook als een aantrekker werken.
Daarom kan een complex systeem oneindig fluctueren en hoeft het niet noodzakelijk naar een evenwicht te convergeren.

Het wordt nog ingewikkelder zodra je je in de aard van de krachten verdiept die het systeem voortstuwen of voorttrekken. Geschat in de nabijheid van de evenwichten van een model, worden deze ‘eigenwaarden’ en ‘eigenvectoren’ genoemd (eigen is een Duitse term die vroeger met ‘karakteristiek’ werd vertaald, maar tegenwoordig met ‘eigen’). Eigenwaarden vertellen je hoe sterk de krachten het systeem naar een evenwicht toe trekken, of ervan weg duwen, en eigenvectoren geven inzicht in de oriëntatie van dat duwen of trekken.
Eigenwaarden worden afgeleid door de vergelijkingen van het systeem in een matrix te zetten, teneinde de krachten die op een positie dicht bij de evenwichten van de matrixvergelijking worden uitgeoefend, vervolgens in de vorm van een polynoom uit te drukken – een vergelijking als x, x2, x3 enzovoort. Door deze vergelijking in factoren te ontbinden met alleen de termen in x krijg je de eigenwaarden van een model. Die eigenwaarden kunnen positief zijn. In dat geval zullen ze het systeem uit zijn evenwicht ‘wegstoten’. Ze kunnen ook negatief zijn. In dat geval zullen ze het evenwicht ‘aantrekken’ of ‘complexificeren’, waardoor ze cycli veroorzaken. Complexe getallen zijn de factoren van kwadratische termen zoals bijvoorbeeld (x2 + 1), waarbij de wortels de vierkantswortel van min één inhouden.
De complexe eigenwaarden, die cyclisch gedrag veroorzaken, hebben ook een reëel getal in zich, dat negatief, positief of nul kan zijn.
Is het reële getal negatief, dan zal de cyclus naar het evenwicht convergeren; is het positief, dan zal het systeem van het evenwicht weg bewegen. Is het nul, dan zal het systeem rond het evenwicht bewegen, maar er niet dichter bij komen en er ook niet verder van weg gaan.
Het plus- of minteken van het grootste reële getal geeft de ‘dominante’ eigenwaarde van het systeem aan.

Het algehele gedrag van een model nabij een evenwicht hangt af van de interactie van al zijn eigenwaarden, en de belangrijkste kwestie hier is het plus- of minteken van het grootste reële getal, dat de ‘dominante’ eigenwaarde van het systeem aangeeft. Is het een minteken, dan is het evenwicht stabiel, en als het systeem dicht genoeg bij het evenwicht begint, zal het er na verloop van tijd naartoe convergeren. Betreft het een plusteken, dan is het evenwicht instabiel en zal het systeem er in de loop van de tijd van weg bewegen. Het krachtenevenwicht hangt ook af van hoe ver het systeem van evenwicht is, hetgeen gedefinieerd wordt in termen van zijn ‘aantrekkingsbassin’ en ‘Lyapunov-functie’ – zie* figuur 4 voor een voorbeeld van hoe deze stabiliteitsanalyse op het model kan worden toegepast. Zoals ik al zei, het is ingewikkeld (neem vooral nog een koffiepauze wanneer het je duizelt).
Het model in figuur 4 heeft twee betekenisvolle evenwichten, waarbij er een als het ‘goede’ evenwicht te boek staat.* Dit evenwicht kent een positieve werkgelegenheidsgraad, een positief loonaandeel in de output en een eindige schuldgraad (het andere, ‘slechte’ evenwicht kent nul werkgelegenheid, nul loonaandeel en een oneindige schuldgraad). De gelineariseerde vergelijking voor het goede evenwicht heeft één negatieve eigenwaarde – wat wil zeggen dat het systeem naar het evenwicht toe wordt getrokken – en één paar complexe eigenwaarden (complexe eigenwaarden treden altijd paarsgewijs op).
Voor de lage waardes van de parameter die de hellingsgraad van de investeringsfunctie bepaalt, hebben deze complexe eigenwaarden nul als hun reële deel. Dit maakt nul tot de ‘dominante’ eigenwaarde aangezien nul groter is dan een negatief getal, maar omdat nul noch aantrekt noch afstoot, kan de negatieve reële eigenwaarde het systeem in de loop van de tijd nog steeds in de richting van het evenwicht duwen.
Bij hogere waardes van de parameter die de hellingsgraad van de investeringsfunctie bepaalt, wordt het reële deel van de complexe eigenwaarden daarentegen positief. Zodra dat gebeurt is het over en uit met de stabiliteit van het ‘goede’ evenwicht. Wanneer het systeem voldoende ver van evenwicht is, domineren de niet-lineaire krachten die het systeem van zijn beginpunt (dat wil zeggen zijn ‘aanvangstoestand’) naar het evenwicht sleuren. Ook neemt de omvang van de cycli af. Maar naarmate het systeem het evenwicht nadert, domineren de lineaire krachten, en heeft de positieve component van de complexe eigenwaarde de overhand over de negatieve component van de reële eigenwaarde. Het systeem begint weg te bewegen van het evenwicht, en de cycli nemen in omvang toe in plaats van af. Dat is wat we in het model in figuur 4 zien gebeuren, en dit is wat er in een simulatie van mijn oorspronkelijke model optrad, voordat ik de stabiliteitskenmerken ervan uitwerkte met de hier* beschreven technieken.7
Deze voorspelling rolde níet uit Minsky’s verbale model, ondanks zijn befaamde opmerking dat ‘stabiliteit – of kalmte – in een wereld met én een cyclisch verleden én kapitalistische financiële instellingen destabiliserend werkt’.*
Minsky’s opmerking had betrekking op een enkele cyclus, niet op het patroon van cycli in de tijd.

Toen ik dit model in augustus 1992 voor het eerst construeerde, was dit fenomeen van af- en dan weer toenemende cycli in vele opzichten het meest verrassende kenmerk ervan, en ik besloot mijn artikel met wat ik toen als een fraaie retorische uitsmijter zag:
'Vanuit het oogpunt van de economische theorie en het economisch beleid vereist deze visie van een kapitalistische economie plus geldmiddelen dat we de denkwijze overstijgen die Keynes zo goed omschreven heeft, namelijk die van een overdreven vertrouwen op het (stabiele) recente verleden als leidraad voor de toekomst. De chaotische dynamiek die in dit artikel beschreven is, moeten we als een waarschuwing opvatten om een periode van relatieve rust in een kapitalistische economie als niets anders dan een stilte voor de storm aan te zien.'*
Tot mijn grote verbazing begon de echte wereld op dat moment mijn model na te bootsen. Vanaf 1980 ging elke nieuwe recessie gepaard met een lagere piek in de werkloosheid,* en elke nieuwe hausse met een lagere piek in de inflatie, terwijl de particuliere schuld veel sneller steeg dan het bbp – zie figuur 5.
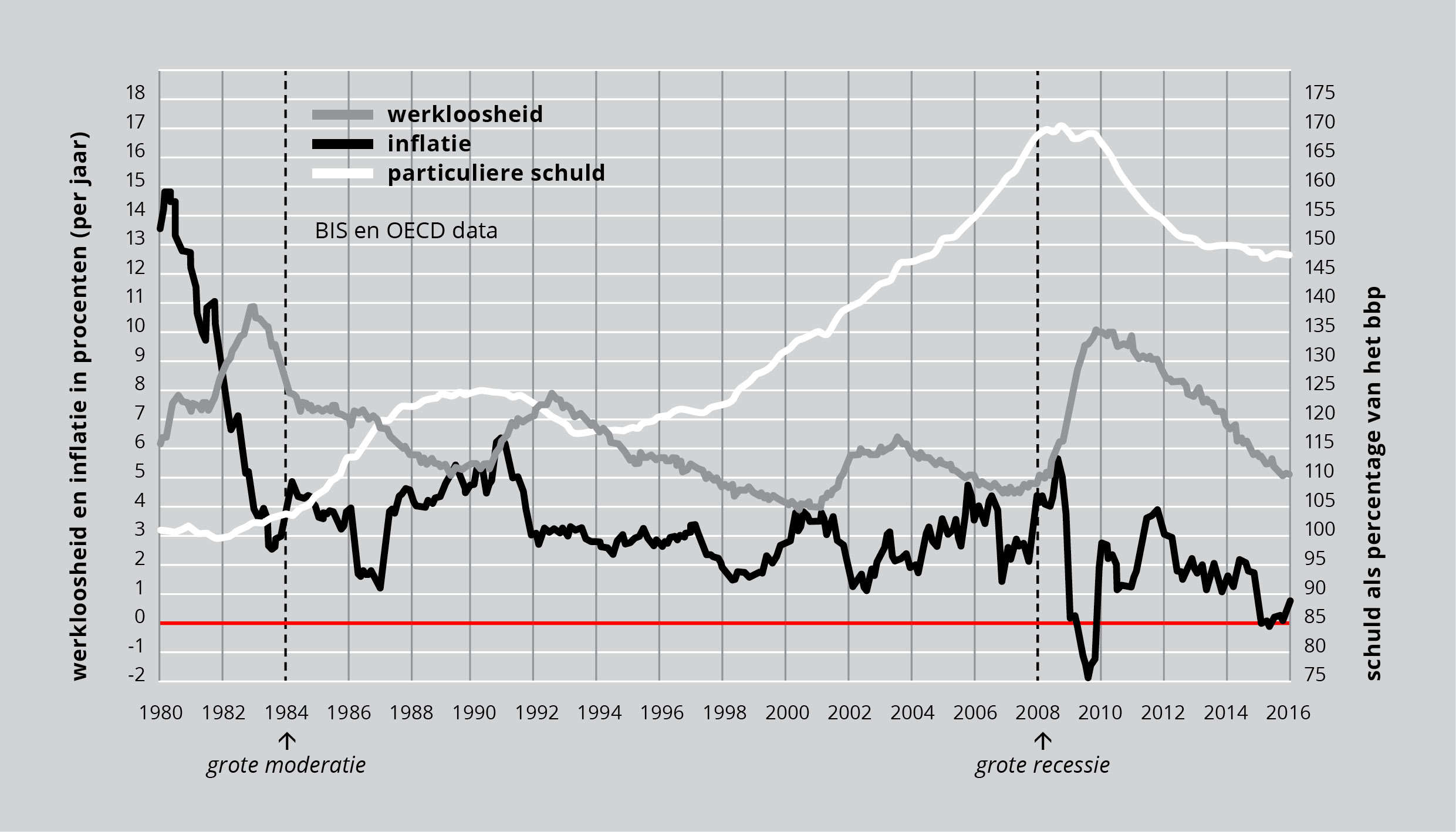
Figuur 5: Afvlakkende cycli in werkgelegenheid en inflatie, terwijl de particuliere schuld als percentage van het bbp toeneemt (gebaseerd op data van de BIS en de OECD).
Met hun lineaire, op evenwicht gefixeerde modelbenadering zagen de neoklassieke economen dit verschijnsel als een rechtvaardiging van hun economische theorie en het daarop gebaseerde beleid, en in hun modellen extrapoleerden zij deze trend naar de toekomst. Ze bestempelden de afname van de economische volatiliteit als de 'Grote Moderatie' en schreven die toe aan hun economisch beleid, dat de nadruk legde op het terugdringen van de inflatie door middel van de controle van de korte rente door de Federal Reserve. Met name Ben Bernanke, toenmalig lid van de Raad van Bestuur van de Federal Reserve, was zeer gul in zijn lofuitingen aan het adres van de Grote Moderatie:
'Zoals gebleken is, heeft het tijdperk van lage inflatie gedurende de afgelopen twee decennia niet alleen geleid tot een aanzienlijke verbetering van de productiviteit en de economische groei, maar, zowel in de VS als daarbuiten, ook tot een beduidende afname van de economische volatiliteit – een verschijnsel dat de "Grote Moderatie" wordt genoemd. Recessies komen minder vaak voor en zijn milder geworden. Ook is de volatiliteit van de productie en de werkgelegenheid op kwartaalbasis aanzienlijk teruggelopen.
'[…] Er zijn aanwijzingen voor de zienswijze dat een betere beheersing van de inflatie in belangrijke mate heeft bijgedragen aan deze welkome verandering in de economie.'*

Mijn reactie hierop luidde dat dit patroon, dat mijn eenvoudige model zo fraai navolgde, de voorbode was van een toekomstige crisis. Die crisis kwam er ook, eind 2007, en ze zou – voor Covid-19 – uitdraaien op de ernstigste economische crisis sinds de Grote Depressie. De werkloosheid schoot omhoog tot boven het niveau van alle voorgaande recessies sinds de Tweede Wereldoorlog,9 terwijl de inflatie plaats maakte voor deflatie.
Deze crisis zou de neoklassieke economen volkomen overvallen. In de nasleep ervan gaven ze weliswaar toe dat hun modellen enige zwakke punten vertoonden, toch zagen zij geen alternatief voor hun kernbenadering, die uit hun pogingen bestond om macro-economische modellen af te leiden uit de grondslag van de micro-economie – een praktijk waarvoor ze de term ‘microgrondslagen’ muntten.
‘Het streven naar een algemeen aanvaarde analytische macro-economische kern, waarin discussies en uitbreidingen kunnen worden ondergebracht, is misschien een utopie, maar het is zeker de moeite van het nastreven waard. […] Het is zonder meer essentieel om uit te gaan van expliciete microgrondslagen; waar zou je anders moeten beginnen?’*
In de jaren tachtig van de vorige eeuw kreeg de overtuiging dat macro-economische theorieën moesten worden afgeleid van micro-economische vaste voet aan de grond, toen de tot dan toe dominante macro-economische ‘IS-LM’-modellen‘ werden vervangen door ‘Reële businesscycle’-modellen, die rechtstreeks waren afgeleid van de micro-economische concepten van naar nutsmaximalisatie strevende consumenten en naar winstmaximalisatie strevende bedrijven. Zoals de toenmalige voorzitter van de American Economic Association Robert Lucas het uitdrukte: ‘Niemand was tevreden met IS-LM als het eindpunt van de macro-economische theorievorming. Ons idee was dat we haar zouden gaan verbinden met micro-economische theorievorming en dat dat de taak van onze generatie was.’*
De complexiteitstheorie heeft echter aangetoond dat de overtuiging, dat macro-economische theorieën uit micro-economische moeten worden afgeleid, onjuist is.

Doe jezelf een plezier en lees eerst een van de beste, meest toegankelijke en prikkelende artikelen die ooit uit de pen van een wetenschapper is gevloeid. Het gaat om 'More is Different'* van de Nobelprijswinnaar voor natuurkunde Philip Anderson. Het stuk zelf kwam voort uit een methodologisch dispuut binnen de natuurkunde over de rol van het 'reductionisme' binnen de wetenschap. Reductionisme is de praktijk van het ontrafelen van een gecompliceerd vakgebied door het op te splitsen in afzonderlijke bestanddelen, deze onafhankelijk van elkaar te begrijpen en vervolgens je kennis over het geheel uit deze bestanddelen op te bouwen. Anderson erkende het succes van het reductionisme, dat ons in staat heeft gesteld de moderne wetenschap te ontwikkelen, maar hij wees er ook op dat reductionisme niet noodzakelijkerwijs ook 'constructionisme' inhoudt:
'Het vermogen om alles te herleiden tot eenvoudige fundamentele wetten impliceert niet het vermogen om die wetten als uitgangspunt te nemen voor het reconstrueren van het universum.'*
Als een van de oorspronkelijke onderzoekers die complexe systeemverschijnselen in de wetenschap ontdekt heeft, merkte Anderson op dat waar het 'constructionisme' bij eenvoudige systemen met eenvoudige (vaak lineaire) relaties tussen de onderdelen prima functioneert, maar dat:
'[…] de constructionistische hypothese tekortschiet zodra die geconfronteerd wordt met het dubbele probleem van schaal en complexiteit. Het gedrag van grote en complexe aggregaten van elementaire deeltjes, zo blijkt, kan niet worden begrepen in termen van een eenvoudige extrapolatie van de eigenschappen van enkele deeltjes. Op elk niveau van complexiteit verschijnen in plaats daarvan geheel nieuwe eigenschappen, en het begrijpen van die nieuwe gedragingen vereist onderzoek dat naar mijn mening net zo fundamenteel van aard is als om het even welk ander onderzoek.'*
Verder merkte Anderson op dat het mogelijk was om de wetenschappen te rangschikken volgens het principe dat 'De elementaire entiteiten van wetenschap X aan de wetten gehoorzamen van wetenschap Y':

Figuur 6: Hiërarchie van elementaire entiteiten.
'Maar deze hiërarchie wil niet zeggen dat wetenschap X slechts 'toegepaste' Y is. In elk stadium zijn geheel nieuwe wetten, begrippen en generalisaties nodig, die evenveel inspiratie en creativiteit vereisen als in het vorige stadium. Psychologie is geen toegepaste biologie net zomin als biologie toegepaste scheikunde is.'*
Doorsnee economen worden echter gedreven door de overtuiging dat macro-economie 'niets anders' zou moeten zijn dan toegepaste micro-economie: de verwezenlijking hiervan heeft de afgelopen dertig jaar hun onderzoeksagenda bepaalt.

Algemeen gesproken is het idee dat macro-economie 'niets anders' is dan toegepaste micro-economie een onverstandig uitgangspunt. Stel bijvoorbeeld dat in de biologie een gelijkaardige overtuiging de overhand zou krijgen en biologen tot de slotsom zouden komen dat moleculaire biologie 'niets anders' is dan toegepaste scheikunde. Dan zou het voor moleculair biologen plots een valide laboratoriumproject zijn om leven uit fundamentele chemische stoffen te creëren. Dat is natuurlijk onmogelijk: ondanks alle kennis die scheikundigen tegenwoordig over scheikundige processen hebben, en biologen over biologische processen, weet niemand hoe je een bergje chemicaliën in een levensvorm kunt veranderen, hoewel dat in het verre verleden op Aarde duidelijk wel is gebeurd.* Daarom is het niet mogelijk om biologie tot toegepaste scheikunde te reduceren: zouden scheikundigen erop staan dat de biologische wetenschap wel aan deze norm voldoet, dan zou er van een biologische wetenschap überhaupt geen sprake zijn.
Juist in de economische wetenschap hebben nota bene economen allang aangetoond dat deze doelstelling (van het herleiden van de macro-economie tot toegepaste micro-economie) niet mogelijk is. In een bekend maar misleidend geïnterpreteerd resultaat, het 'Sonnenschein Mantel Debreu'-theorema genoemd,* stelden econometristen de vraag of het mogelijk is om een neerwaarts aflopende marktvraagcurve af te leiden uit het aggregaat van een groot aantal individuele, neerwaarts aflopende vraagcurves. Hun conclusie luidde dat dit niet mogelijk was, ténzij je aannam, om de eerste econoom aan te halen die dit resultaat heeft afgeleid, dat 'de Engelcurven voor verschillende individuen bij dezelfde prijzen parallelle rechte lijnen zijn'.* Ontdaan van economenjargon verduidelijkte Gorman zijn conclusie met de volgende veelzeggende bewering:
'De hierboven geciteerde noodzakelijke en voldoende voorwaarde is intuïtief redelijk. Ze wil zoveel zeggen dat een extra eenheid aan koopkracht op dezelfde manier moet worden besteed, ongeacht aan wie die gegeven wordt.'*
Er is niets 'intuïtief redelijks' aan deze voorwaarde: in feite zegt die dat Elon Musk een extra euro aan precies dezelfde zaken zal uitgeven als een dakloze met die euro zou kopen. Dat is niet alleen overduidelijk onjuist maar ook intuïtief onredelijk, dus waarom beweert Gorman dan precies het tegenovergestelde?
De reden is dat áls de inkomensverdeling van invloed is op de consumptie, hetgeen duidelijk het geval is, de marktvraagcurve – die kan worden afgeleid door de neerwaarts aflopende individuele vraagcurves van een heleboel individuen te aggregeren – elke willekeurige vorm kan aannemen en helemaal niet noodzakelijk neerwaarts aflopend hoeft te zijn. Deze ontdekking draait de hele theorie van 'vraag en aanbod' de nek om. Zoals andere onderzoekers op dit gebied het stelden: 'De nutshypothese vertelt ons niets over de marktvraag tenzij deze wordt aangevuld met bijkomende vereisten.'*
Dit is een klassieke 'emergente' eigenschap. Niet alleen kan de macro-economie niet worden afgeleid uit de micro-economie, zelfs het model van een marktvraagcurve kan niet worden afgeleid – dat wil zeggen, met de eigenschappen die neoklassieke economen willen dat het model heeft – uit het model van een enkele consument. De zoektocht naar een micro-economische grondslag voor macro-economie is dus zinloos.
Een zoektocht naar stevige fundamenten is daarentegen wel zinvol. Hoe zouden zulke fundamenten eruit kunnen zien?

Hoewel het misschien paradoxaal klinkt, kan een macro-economische theorievorming rechtstreeks uit zichzelf worden afgeleid.
De macro-economie gaat namelijk over economische aggregaten, en een groot deel ervan betreft verhoudingen van het ene aggregaat tot het andere. We maken ons zorgen over het werkloosheidspercentage, dat wil zeggen over de verhouding tussen het aantal werklozen en de beroepsbevolking; bij de inkomensverdeling gaat het erom welk deel van het totale inkomen naar welke groepen gaat; en bij het groeitempo van de economie draait het om de verhouding tussen de bbp-stijging (of -daling) en het huidige niveau. Deze macro-economische aggregaten en hun verhoudingen tot elkaar bepalen het vakgebied, en een dynamische macro-economische theorievorming kan worden afgeleid door deze definities simpelweg om te zetten in uitspraken over veranderingen in de tijd.
Met andere woorden, de structuur van de economie bepaalt in grote mate hoe zij zich gedraagt. Deze structuur is in belangrijke mate gecodificeerd in de macro-economische definities zelf. Door eenvoudigweg de kerndefinities te selecteren en deze in dynamische uitspraken om te zetten, kunnen we de grondslagen voor de macro-economische theorievorming leggen. Naarmate we de definities uitbreiden – bijvoorbeeld door het bbp niet langer als een eenvoudig cijfer op te vatten, maar als een reeks industrietakken die een reeks producten voortbrengen – zal de wiskundige vorm van die uitgebreide definitie ons een nog rijker model opleveren. Het is niet nodig om terug te grijpen op de micro-economie, laat staan de macrogrondslagen te baseren op die van de microgrondslagen. Daarbij komt dat vrijwel alle conventionele microgrondslagen, zoals ik in Debunking Economics* uitleg, toch al onzin zijn.
Ga nog even terug naar het model van Minsky’s ‘Financiële Instabiliteitshypothese’ dat in figuur 4 is weergegeven. De drie belangrijkste ratio’s in dat model zijn de werkgelegenheidsgraad, het aandeel van de lonen in het bbp en de schuldgraad:
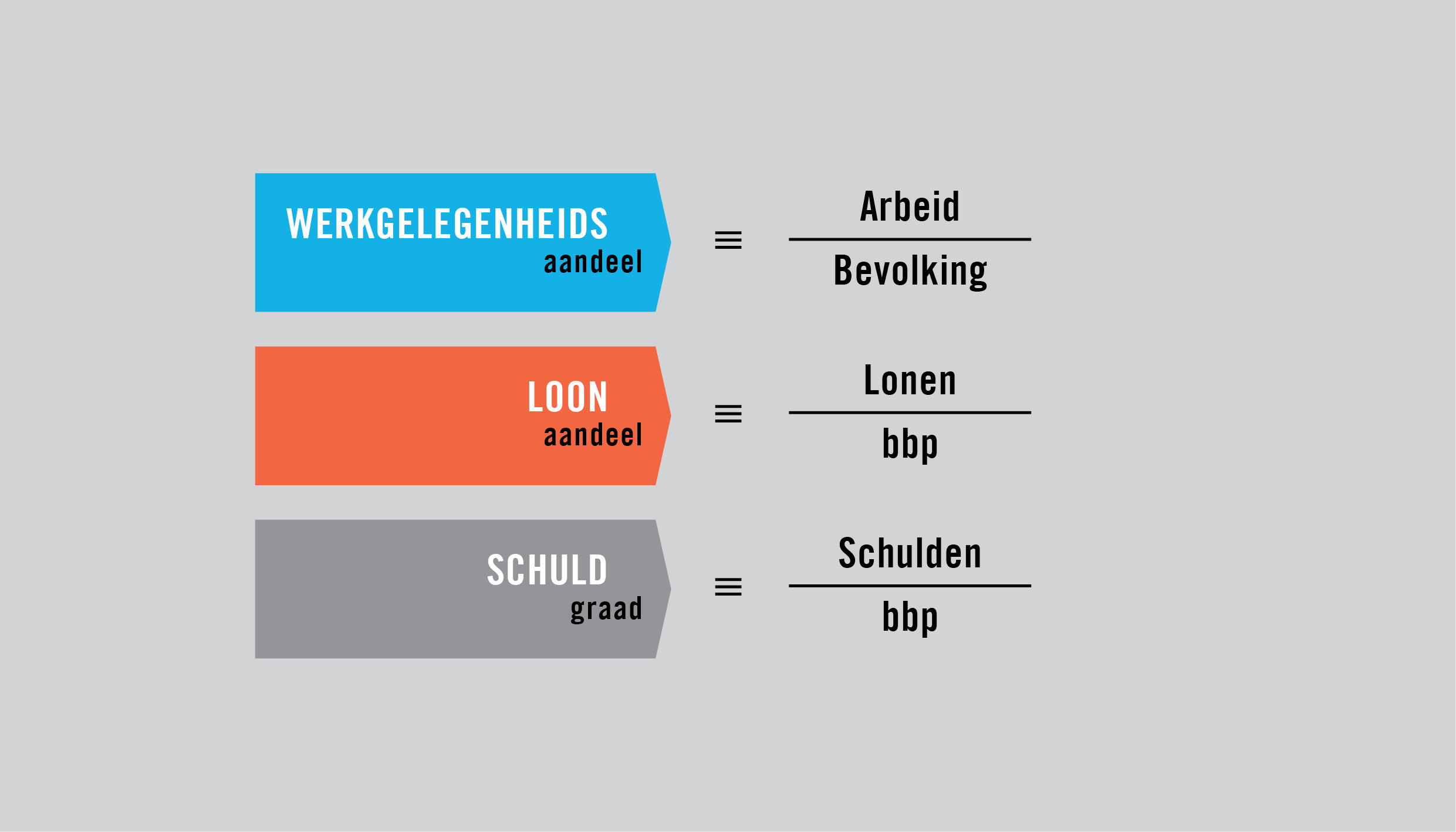
Vergelijking 1
In hun huidige vorm zijn dit ‘statische’ definities: ze definiëren verhoudingen die onveranderlijk geldig zijn, maar ze beschrijven niet het veranderingsproces van die verhoudingen in de loop van de tijd.
Toch is het mogelijk om tot uitspraken te komen over dat veranderingsproces door die uitspraken ‘simpelweg’ te differentiëren ten opzichte van de factor tijd.

Voor mensen die de taal van de wiskunde 'spreken' is het dynamisch maken van die uitspraken allemaal niet zo lastig. Kan je dat niet, dan bestaat er gelukkig een simpele truc met percentages die dit een stuk eenvoudiger maakt: de procentuele veranderingsgraad van een verhouding is gelijk aan de procentuele veranderingsgraad van de teller minus de procentuele veranderingsgraad van de noemer. Op dezelfde manier is de procentuele veranderingsgraad van een product (zeg, Lonen gedefinieerd als het Loontarief maal Arbeid) de som van de procentuele veranderingspercentages van de twee delen van het product.
Dus door gewoon naar de definities in vergelijking 1 te kijken, kunnen we ze in een dynamische vorm schrijven:
• De procentuele veranderingsgraad van de werkgelegenheidsgraad is gelijk aan de procentuele veranderingsgraad van de beroepsbevolking minus de procentuele veranderingsgraad van de bevolkingsgroei;
• De procentuele veranderingsgraad van het aandeel van de lonen in het bbp is gelijk aan de procentuele veranderingsgraad van de lonen minus de procentuele veranderingsgraad van het bbp; en
• De procentuele veranderingsgraad van de schuldgraad is gelijk aan de procentuele veranderingsgraad van de schuld minus de procentuele veranderingsgraad van het bbp.
Uitgaande van dezelfde functies voor veranderingen in lonen en investeringen als in figuur 4, en van dezelfde hypothese dat investeringen met schulden worden gefinancierd die de winsten overtreffen, leidt dit tot een model dat precies dezelfde dynamiek vertoont. Er zijn problemen met sommige van deze definities, die in meer geavanceerde modellen* aangepakt zullen moeten worden.
Maar net zoals het sterk gestileerde turbulentiemodel van Lorenz een basiselement vormt van de moderne meteorologie, vormt het model dat wij hier ontwikkeld hebben een basiselement voor een waarlijk moderne macro-economische theorie.
Een waarlijk moderne macro-economische theorie waar geen greintje 'microgrondslag' bij te pas gekomen.

Ook was het niet al te ingewikkeld om dit model te construeren, zeker wanneer je dat vergelijkt met het pijnlijk proces dat neoklassieke economen, met gebruikmaking van hun ongeldige ‘microgrondslagen’-benadering, moeten doorlopen om zelfs hun simpelste op evenwicht gefixeerde ‘reële businesscycle’-modellen in elkaar te knutselen – laat staan hun poging tot groter realisme met ‘Dynamische Stochastische Algemene Evenwichtsmodellen’. Zoals de toonaangevende neoklassieke modelleerder Olivier Blanchard het uitdrukt:
‘Het denken in termen van een reeks verstoringen in een concurrerende economie impliceert een lange weg van het concurrentiemodel naar een redelijk plausibele beschrijving van de economie. Maar, nogmaals, ik zou niet weten waar je anders moet beginnen.’*
Het bouwen van ons model vereiste slechts een fractie van al dit nodeloze geploeter, en het kan uitgebreid worden door de gebruikte definities te veralgemeniseren. Zo kan het effect van de inflatie bijvoorbeeld worden meegenomen door het hier gebruikte ‘reële’ bbp te vervangen met het nominale bbp, waarbij het reële bbp gelijk is aan het nominale bbp gedeeld door het prijspeil. Het inflatiepercentage komt dan in 2 van de 3 vergelijkingen van het model voor. De abstractie van één enkel cijfer voor het bbp kan worden vervangen met de realiteit dat het bbp in werkelijkheid de som van de outputs van talrijke verschillende industrietakken is. Naast schuld die wordt aangegaan om investeringen te financieren, kunnen we een categorie introduceren voor een niet-productief ‘ponzi’-achtig gebruik van schuld. Overheidsuitgaven kunnen een plek krijgen, enzovoorts. De macro-economische theorievorming kan haar eigen ontwikkeling sturen zodra we van de constructionistische misvatting afstappen dat ze van micro-economische vooronderstellingen moet worden afgeleid.
Willen we een nieuwe grondslag voor de macro-economische theorievorming leggen, dan moet die tot slot verband houden met de fundamentele fysica van hoe onze beschaving de minerale en biologische bijdragen die de biosfeer ons levert, omzet in de industriële producten die we verbruiken, en het afval dat we noodzakelijkerwijs weer in de biosfeer dumpen. Neoklassieke economen hebben dat nooit gedaan, en kunnen dat tot op grote hoogte ook niet doen. Maar dat is het thema van de volgende hoofdstuk in het boek The New Economics: A Manifesto.
Gerelateerd
Ecologie:
• Het principe van maximaal vermogen in de evolutie, ecologie en economie
Economie:
• Economisch denken voor de toekomst – voorbij het superorganisme
• Eindspel: de economie als ecologische ramp en wat er moet veranderen
• Drie contradicties van het kapitalisme
Complexiteit:
• De natuur van de economie
Ontwrichting:
• Kunnen we ontsnappen aan de energie-complexiteitsspiraal?


